题目内容
3.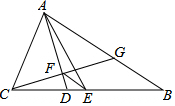 如图,在△ABC中,AB=5,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.
如图,在△ABC中,AB=5,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.
分析 首先证明△ACG是等腰三角形,则AG=AC=3,FG=CF,则EF是△BCG的中位线,利用三角形的中位线定理即可求解.
解答 解:∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形,
∴AG=AC,
∵AC=3,
∴AG=AC=3,FG=CF,
∵AE为△ABC的中线,
∴EF是△BCG的中位线,
∴EF=$\frac{1}{2}$BG,
∵AB=5,
∴BG=AB-AG=5-3=2.
∴EF=1.
故答案为1.
点评 本题考查了三角形的中位线定理以及等腰三角形的判定与性质,正确证明FG=CF是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
5.2015年10月5日我国药学家屠呦呦因研发抗疟疾药物-青蒿素而获得诺贝尔医学奖,自1990年至2015年,全世界因防治得当,共有2220万新发疟疾患者的生命得到拯救,其中2220万用科学记数法表示为( )
| A. | 222.0×104 | B. | 22.2×106 | C. | 2.22×107 | D. | 2.22×108 |
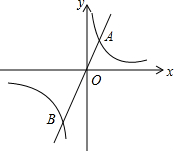 如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4.
如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4.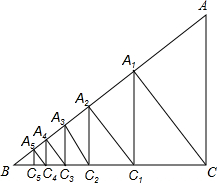 如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.
如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.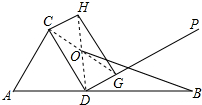 如图,线段AB的长为10cm,点D在AB上,△ACD为等边三角形,过点D作DP⊥CD,点G是DP上不与点D重合的一动点,作矩形CDGH.记矩形CDGH的对角线交点为O,连接OA、OB,
如图,线段AB的长为10cm,点D在AB上,△ACD为等边三角形,过点D作DP⊥CD,点G是DP上不与点D重合的一动点,作矩形CDGH.记矩形CDGH的对角线交点为O,连接OA、OB,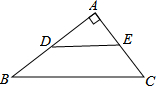 如图,在△ABC中,∠A=90°,AB=20cm,AC=12cm,点D从点B出发以3cm/秒的速度向点A运动,同时点E从点A出发以2cm/秒的速度向点C运动,其中一个点到达终点时,另一点也随之停止运动,当∠ADE=45°时,运动的时间是( )
如图,在△ABC中,∠A=90°,AB=20cm,AC=12cm,点D从点B出发以3cm/秒的速度向点A运动,同时点E从点A出发以2cm/秒的速度向点C运动,其中一个点到达终点时,另一点也随之停止运动,当∠ADE=45°时,运动的时间是( )