题目内容
10.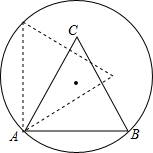 如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.
如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.
分析 设圆心为O,点C的对应点为C′,连接OA、OB、OC′,利用勾股定理逆定理求出∠AOC′=∠AOB=90°,从而判断出点B、O、C′三点共线,然后根据直径所对的圆周角是直角求出∠BAC′=90°,再根据点C转过的度数=∠BAC′-∠BAC代入数据计算即可得解.
解答  解:如图设圆心为O,点C的对应点为C′,连接OA、OB、OC′,
解:如图设圆心为O,点C的对应点为C′,连接OA、OB、OC′,
∵正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,
∴AO2+C′O2=($\frac{\sqrt{2}}{2}$)2+($\frac{\sqrt{2}}{2}$)2=$\frac{1}{2}$+$\frac{1}{2}$=1,
∴AO2+C′O2=AC′2,
∴∠AOC′=90°,
同理可得∠AOB=90°,
∴∠AOC′=∠AOB=90°,
∴点B、O、C′三点共线,
∴∠BAC′=90°,
又∵△ABC是等边三角形,
∴∠BAC=60°,
∴点C转过的度数=∠BAC′-∠BAC=90°-60°=30°.
故答案为:30°.
点评 本题考查了旋转的性质,等边三角形的性质,勾股定理逆定理,解答本题关键在于巧妙计算出点B、O、C′三点共线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
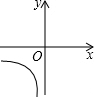 如图是反比例函数y=$\frac{k+5}{x}$的图象的一支,根据图象回答下列问题:
如图是反比例函数y=$\frac{k+5}{x}$的图象的一支,根据图象回答下列问题: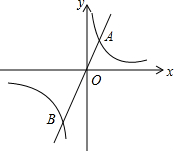 如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4.
如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4. 一个大正方形和四个全等的小正方形按图①、图②两种方式摆放,根据图中数据,则图②的大正方形中未被小正方形覆盖部分的面积大小为24.
一个大正方形和四个全等的小正方形按图①、图②两种方式摆放,根据图中数据,则图②的大正方形中未被小正方形覆盖部分的面积大小为24.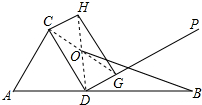 如图,线段AB的长为10cm,点D在AB上,△ACD为等边三角形,过点D作DP⊥CD,点G是DP上不与点D重合的一动点,作矩形CDGH.记矩形CDGH的对角线交点为O,连接OA、OB,
如图,线段AB的长为10cm,点D在AB上,△ACD为等边三角形,过点D作DP⊥CD,点G是DP上不与点D重合的一动点,作矩形CDGH.记矩形CDGH的对角线交点为O,连接OA、OB, 如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$.
如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$. 如图,已知在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20.
如图,已知在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20.