题目内容
12．若一个正多边形的一个内角等于140°，那么这个多边形是正九边形．分析 一个正多边形的每个内角都相等，根据内角与外角互为邻补角，因而就可以求出外角的度数．根据任何多边形的外角和都是360°，利用360°除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．
解答 解：∵内角与外角互为邻补角，
∴正多边形的一个外角是180°-140°=40°，
∵多边形外角和为360°，
∴360°÷40°=9，
则这个多边形是九边形．
故答案为：九．
点评 本题考查了多边形的内角与外角，解决本题的关键是由外角和求正多边形的边数．
练习册系列答案
相关题目
2．
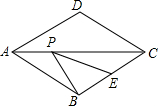如图，在菱形ABCD中，AD=2，∠ABC=120°，E是BC的中点，P为对角线AC上的一个动点，则PE+PB的最小值为（ ）
如图，在菱形ABCD中，AD=2，∠ABC=120°，E是BC的中点，P为对角线AC上的一个动点，则PE+PB的最小值为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | 1 | D． | 5 |
作三角形关于点成中心对称的图形：已知△ABC和点O，画出△DEF，使△DEF与△ABC关于O成中心对称．
1．估计$2\sqrt{6}-1$的值在（ ）
| A． | 2与3之间 | B． | 3与4之间 | C． | 4与5之间 | D． | 5与6之间 |
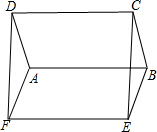如图，?ABCD与?ABEF中，BC=BE，∠ABC=∠ABE，求证：四边形EFDC是矩形．