题目内容
13.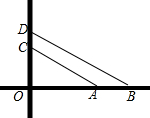 如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )
如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )| A. | 5m | B. | 4m | C. | 3m | D. | 2m |
分析 在RT△AOC中根据勾股定理求出OA的长,进而可得OB,在RT△BOD中根据勾股定理可得OD的长,可得答案.
解答 解:在RT△AOC中,∵OA2+OC2=AC2,
∴OA=$\sqrt{A{C}^{2}-O{C}^{2}}$=$\sqrt{1{7}^{2}-{8}^{2}}$=15(m),
∴OB=0A+AB=20m,
在RT△BOD中,∵BD2=OB2+OD2,
∴OD=$\sqrt{B{D}^{2}-O{B}^{2}}$=$\sqrt{(10\sqrt{5})^{2}-2{0}^{2}}$=10(m),
∴CD=OD-OC=2m,
故选:D.
点评 本题主要考查勾股定理的应用,熟练掌握勾股定理内容并加以运用是根本也是关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
1.估计$2\sqrt{6}-1$的值在( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
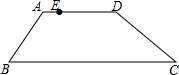 如图,四边形ABCD是梯形,AD∥BC,E为AD上任意一点,∠B+∠C=90°,请先将AB向右平移,使点A与点E重合,交BC于点F,再将CD向作平移,使点D与点E重合,交BC于点G,画出平移后的图形,并判断△EFG的形状.
如图,四边形ABCD是梯形,AD∥BC,E为AD上任意一点,∠B+∠C=90°,请先将AB向右平移,使点A与点E重合,交BC于点F,再将CD向作平移,使点D与点E重合,交BC于点G,画出平移后的图形,并判断△EFG的形状.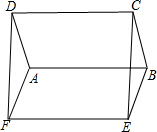 如图,?ABCD与?ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形.
如图,?ABCD与?ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形.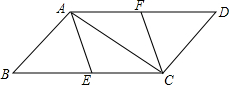 如图,?ABCD中,E,F分别为BC,AD的中点.
如图,?ABCD中,E,F分别为BC,AD的中点.