题目内容
14．
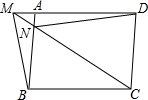如图，已知：?ABCD，M是DA延长线上一点，连接MB，MC，且MC交AB于点N，连接DN，求证：S△BMN=S△AND．
分析 由平行四边形的性质得出△BCM的面积=$\frac{1}{2}$?ABCD的面积，△CDN的面积=$\frac{1}{2}$?ABCD的面积，得出△BMN的面积+△BCN的面积=△BCN的面积+△AND的面积，即可得出结论．
解答 证明：∵四边形ABCD是平行四边形，
∴DM∥BC，AB∥CD，
∴△BCM的面积=$\frac{1}{2}$?ABCD的面积，△CDN的面积=$\frac{1}{2}$?ABCD的面积，
∴△BCN的面积+△AND的面积=$\frac{1}{2}$?ABCD的面积，
∴△BMN的面积+△BCN的面积=△BCN的面积+△AND的面积，
∴S△BMN=S△AND．
点评 本题考查了平行四边形的性质、三角形与平行四边形的面积关系；熟记平行四边形的性质，理解三角形与平行四边形的面积关系是解决问题的关键．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
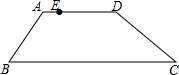如图，四边形ABCD是梯形，AD∥BC，E为AD上任意一点，∠B+∠C=90°，请先将AB向右平移，使点A与点E重合，交BC于点F，再将CD向作平移，使点D与点E重合，交BC于点G，画出平移后的图形，并判断△EFG的形状．
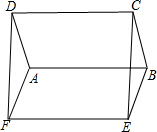如图，?ABCD与?ABEF中，BC=BE，∠ABC=∠ABE，求证：四边形EFDC是矩形．
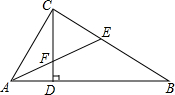如图所示，在△ABC中，∠ACB=90°，高CD和角平分线AE交于点F，求证：CF=CE．
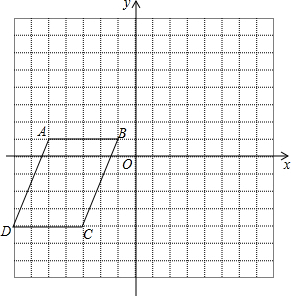四边形ABCD的顶点坐标分别为A（-5，-1），B（-1，-1），C（-3，-4），D（-7，-4），将四边形ABCD先向上平移5个单位长度，再向右平移8个单位长度．
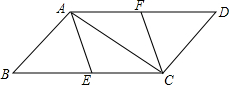如图，?ABCD中，E，F分别为BC，AD的中点．