题目内容
9.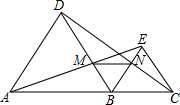 如图,A、B、C三点在同一直线上,△ABD和△BCE都是等边三角形,
如图,A、B、C三点在同一直线上,△ABD和△BCE都是等边三角形,(1)求证:AE=CD;
(2)若AE交BD于M,CD交BE于N,连结MN,试判断△MBN的形状,并说明理由.
分析 (1)根据等边三角形的性质就可以得出△AEB≌△DCB,就可以得出结论;
(2)通过证明△DBN≌△ABM,就可以得出BN=BM,由∠DBE=60°就可以得出结论.
解答 证明:(1)∵△ABD,△BCE都是等边三角形,
∴∠ABD=∠CBE═60°,AB=DB,CB=EB.
∴∠ABD+∠EBD=∠CBE+∠DBE,
即∠ABE=∠DBC.
∵A,B,C在同一直线上,
∴∠ABC=180°,
∴∠DBE=60°.
∴∠ABD=∠EBD.
在△AEB和△DCB中,
$\left\{\begin{array}{l}{AB=DB}\\{∠ABE=∠DBC}\\{CB=EB}\end{array}\right.$,
∴△AEB≌△DCB(SAS),
∴AE=CD.
(2)∵△AEB≌△DCB,
∴∠EAB=∠CDB.
在△DBN和△ABM中,
$\left\{\begin{array}{l}{∠EAB=∠CDB}\\{AB=DB}\\{∠DBE=∠ABM}\end{array}\right.$,
∴△DBN≌△ABM(ASA),
∴BN=BM.
∵∠DBE=60°,
∴△MBN是等边三角形.
点评 本题考查了等边三角形的性质的运用,全等三角形的性质的运用,全等三角形的判定及性质的运用.解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.
如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.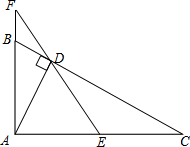 如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证: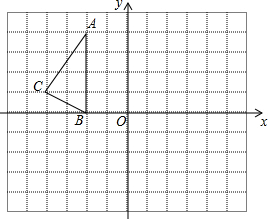 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题: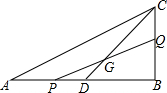 如图,在直角三角形ABC中,∠B=90°,AB=10,BC=5,D是AB的中点,动点Q从点B开始在线段BC上以每秒1个单位的速度向C移动,动点P从点A开始在线段AD上以每秒1个单位的速度向点D移动,设点P,Q的移动时间为t秒,当△DPG与△DAC相似时,求t的值.
如图,在直角三角形ABC中,∠B=90°,AB=10,BC=5,D是AB的中点,动点Q从点B开始在线段BC上以每秒1个单位的速度向C移动,动点P从点A开始在线段AD上以每秒1个单位的速度向点D移动,设点P,Q的移动时间为t秒,当△DPG与△DAC相似时,求t的值.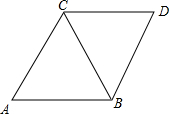 已知:如图,等边三角形ABC与等边三角形DBC的一边BC重合
已知:如图,等边三角形ABC与等边三角形DBC的一边BC重合