题目内容
12.在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,若线段MA绕点M旋转得到线段MA′(1)如图①,当线段MA绕点M逆时针旋转60°时,线段AA′的长=1;
(2)如图②,连接A′C,则A′C长度的最小值是$\sqrt{7}$-1.
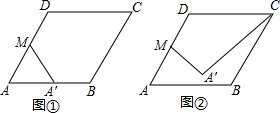
分析 (1)根据旋转的性质可得MA=MA',然后证明△AMA'是等边三角形即可求解;
(2)当A'在MC上时,线段A'C长度最小,作ME⊥CD于点E,首先在直角△DME中利用三角函数求得ED和EM的长,然后在直角△MEC中利用勾股定理求得MC的长,然后减去MA的长即可求解.
解答 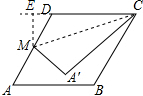 解:(1)∵MA=MA',∠AMA'=60°,
解:(1)∵MA=MA',∠AMA'=60°,
∴△AMA'是等边三角形,
∴AA'=AM=$\frac{1}{2}$AD=1,
故答案是1;
(2)作ME⊥CD于点E.
∵菱形ABCD中,∠A=60°,
∴∠EDM=60°,
在直角△MDE中,DE=MD•cos∠EDM=$\frac{1}{2}$×1=$\frac{1}{2}$,ME=MD•sin∠EDM=$\frac{\sqrt{3}}{2}$,
则EC=CD+ED=2+$\frac{1}{2}$=$\frac{5}{2}$,
在直角△CEM中,MC=$\sqrt{C{E}^{2}+M{E}^{2}}$=$\sqrt{(2+\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{7}$,
当A'在MC上时A'C最小,则A′C长度的最小值是:$\sqrt{7}$-1.
故答案是:$\sqrt{7}$-1.
点评 本题考查了旋转的性质,以及三角函数和勾股定理,正确理解等边三角形判定定理,理解A'C最短的条件是关键.

练习册系列答案
相关题目
3.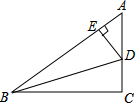 如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
 如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )
如图、已知△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,且AE=3cm,AC=9cm,则△ADE的周长为( )| A. | 11cm | B. | 18cm | C. | 12cm | D. | 6cm |
 如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长.
如图,△ABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,分别求出DE与EC的长. 如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.
如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.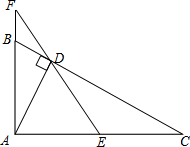 如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证: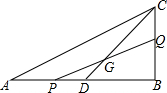 如图,在直角三角形ABC中,∠B=90°,AB=10,BC=5,D是AB的中点,动点Q从点B开始在线段BC上以每秒1个单位的速度向C移动,动点P从点A开始在线段AD上以每秒1个单位的速度向点D移动,设点P,Q的移动时间为t秒,当△DPG与△DAC相似时,求t的值.
如图,在直角三角形ABC中,∠B=90°,AB=10,BC=5,D是AB的中点,动点Q从点B开始在线段BC上以每秒1个单位的速度向C移动,动点P从点A开始在线段AD上以每秒1个单位的速度向点D移动,设点P,Q的移动时间为t秒,当△DPG与△DAC相似时,求t的值.