题目内容
20.若A(a,b)、B(a-1,c)是函数y=-$\frac{1}{x}$图象上的两点,且a<0,则b与c的大小关系为( )| A. | b<c | B. | b=c | C. | b>c | D. | 无法判断 |
分析 根据反比例函数的性质:k<0时,在图象的每一支上,y随x的增大而增大进行分析即可.
解答 解:∵a<0,
∴a-1<0,a>a-1,
∵k=-1<0,
∴在图象的每一支上,y随x的增大而增大,
∵A(a,b)、B(a-1,c)是函数y=-$\frac{1}{x}$图象上的两点,
∴b>c,
故选:C.
点评 此题主要考查了反比例函数图象的性质,关键是掌握反比例函数的性质:
(1)反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
10.关于x的一元二次方程x2+2x-m=0有实数根,则m的取值范围是( )
| A. | m≥-1 | B. | m>-1 | C. | m≤-1 | D. | m<-1 |
15.已知一次函数y=kx+b的图象与直线y=5x+1平行,且过点(2,1),那么此一次函数的解析式为( )
| A. | y=-5x-2 | B. | y=-5x-6 | C. | y=-5x+10 | D. | y=-5x+11 |
5.下列计算正确的是( )
| A. | a3•a3=a9 | B. | (a+b)2=a2+b2 | C. | a2÷a2=0 | D. | (a2)3=a6 |
12.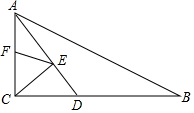 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )| A. | $\frac{40}{3}$ | B. | $\frac{15}{4}$ | C. | $\frac{24}{5}$ | D. | 6 |
9.温州为了推进“中央绿轴”建设,某园林公司增加了人力进行大型树木移植,现在平均每天比原计划多植树50棵,现在植树600棵所需时间与原计划植树400棵所需时间相同,设原计划平均每天植树x棵,则列出的方程为( )
| A. | $\frac{600}{x+50}$=$\frac{400}{x}$ | B. | $\frac{600}{x}$=$\frac{400}{x-50}$ | C. | $\frac{600}{x-50}$=$\frac{400}{x}$ | D. | $\frac{600}{x}$=$\frac{400}{x+50}$ |
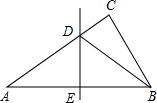 如图,在△ABC中,DE垂直平分AB,交边AC于点D,交边AB于点E,连接BD.若AC=6,△BCD的周长为10,则BC的长为( )
如图,在△ABC中,DE垂直平分AB,交边AC于点D,交边AB于点E,连接BD.若AC=6,△BCD的周长为10,则BC的长为( ) 如图所示,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C(0,4),且此抛物线顶点为D(1,$\frac{9}{2}$).
如图所示,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C(0,4),且此抛物线顶点为D(1,$\frac{9}{2}$).