题目内容
10.关于x的一元二次方程x2+2x-m=0有实数根,则m的取值范围是( )| A. | m≥-1 | B. | m>-1 | C. | m≤-1 | D. | m<-1 |
分析 根据方程的系数结合根的判别式,即可得出△=4+4m≥0,解之即可得出结论.
解答 解:∵关于x的一元二次方程x2+2x-m=0有实数根,
∴△=22-4×1×(-m)=4+4m≥0,
解得:m≥-1.
故选A.
点评 本题考查了根的判别式,牢记“当△≥0时,方程有实数根”是解题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | (2x3y)2=4x6y2 | B. | $\sqrt{(-4)×(-6)}$=$\sqrt{-4}$×$\sqrt{-6}$ | C. | x8÷x4=x2 | D. | -16(x-2)=-16x-32 |
5.计算a3×(-a)5的结果是( )
| A. | a8 | B. | -a8 | C. | a15 | D. | -a15 |
2.-2的倒数是( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | |-$\frac{1}{2}$| |
20.若A(a,b)、B(a-1,c)是函数y=-$\frac{1}{x}$图象上的两点,且a<0,则b与c的大小关系为( )
| A. | b<c | B. | b=c | C. | b>c | D. | 无法判断 |
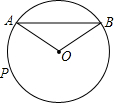 如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°
如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°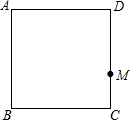 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.