题目内容
9.温州为了推进“中央绿轴”建设,某园林公司增加了人力进行大型树木移植,现在平均每天比原计划多植树50棵,现在植树600棵所需时间与原计划植树400棵所需时间相同,设原计划平均每天植树x棵,则列出的方程为( )| A. | $\frac{600}{x+50}$=$\frac{400}{x}$ | B. | $\frac{600}{x}$=$\frac{400}{x-50}$ | C. | $\frac{600}{x-50}$=$\frac{400}{x}$ | D. | $\frac{600}{x}$=$\frac{400}{x+50}$ |
分析 设原计划平均每天植树棵x棵,根据“现在植树600棵所需的时间与原计划植树400棵所需的时间相同”这一等量关系列出分式方程求解即可.
解答 解:设原计划平均每天植树棵x棵,现在每天植树(x+50)棵,
依题意得,$\frac{600}{x+50}$=$\frac{400}{x}$.
故选:A.
点评 此题考查了由实际问题列分式方程,关键在寻找相等关系,列出方程.

练习册系列答案
相关题目
20.若A(a,b)、B(a-1,c)是函数y=-$\frac{1}{x}$图象上的两点,且a<0,则b与c的大小关系为( )
| A. | b<c | B. | b=c | C. | b>c | D. | 无法判断 |
17. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )| A. | 240米 | B. | 160米 | C. | 150米 | D. | 140米 |
14.某地组织20辆汽车装运A,B,C三种苹果42吨到外地销售.按规定每辆车只装一种苹果,且必须装满,每种苹果不少于2车.
(1)设用x辆车装运A种苹果,用y辆车装运B种苹果.根据上表提供的信息,求y与x之间的函数关系式,并求出x的取值范围;
(2)设此次外销活动的利润为W(百元),求W与x之间的函数关系式,x为何值时W(百元)取得最大利润,并安排此时相应的车辆调配方案.
| 苹果品种 | A | B | C |
| 每辆汽车(吨) | 2.2 | 2.1 | 2 |
| 每吨苹果获利(百元) | 6 | 8 | 5 |
(2)设此次外销活动的利润为W(百元),求W与x之间的函数关系式,x为何值时W(百元)取得最大利润,并安排此时相应的车辆调配方案.
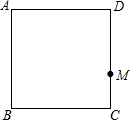 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.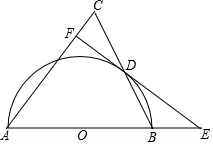 如图,△ABC是等腰三角形,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线,与AB的延长线交于点E,与AC交于点F.
如图,△ABC是等腰三角形,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线,与AB的延长线交于点E,与AC交于点F.