题目内容
 如图,△ABC为等边三角形,BD⊥AC于点D,点E在BC的延长线上,CE=CD,△ABC的周长为6,BD=
如图,△ABC为等边三角形,BD⊥AC于点D,点E在BC的延长线上,CE=CD,△ABC的周长为6,BD=| 3 |
考点:等边三角形的性质
专题:
分析:根据等边三角形的性质可得∠ACB=60°,∠CBD=30°根据勾股定理即可求得CD=1,BC=2,再根据等边对等角的性质求出∠E=∠CDE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式求解得到∠E=30°,从而得到∠E=∠CBD,再根据等角对等边的性质即可得出BD=DE=
,进而求得三角形的周长.
| 3 |
解答:证明:∵△ABC是等边三角形,D是AC中点,
∴∠ACB=60°,∠CBD=30°,∠BDC=90°,
∴BC=2DC,
∵BD=
,
∵BC2=BD2+DC2,即4DC2=3+DC2,
∴CD=1,BC=2,
∵CD=CE,
∴∠E=∠CDE,CE=1,
∵∠BCD=∠E+∠CDE=2∠E=60°,
∴∠E=30°,
∴∠E=∠CBD,
∴BD=DE=
,
∴△BDE的周长=BD+DE+BC+CE=
+
+2+1=3+2
.
∴∠ACB=60°,∠CBD=30°,∠BDC=90°,
∴BC=2DC,
∵BD=
| 3 |
∵BC2=BD2+DC2,即4DC2=3+DC2,
∴CD=1,BC=2,
∵CD=CE,
∴∠E=∠CDE,CE=1,
∵∠BCD=∠E+∠CDE=2∠E=60°,
∴∠E=30°,
∴∠E=∠CBD,
∴BD=DE=
| 3 |
∴△BDE的周长=BD+DE+BC+CE=
| 3 |
| 3 |
| 3 |
点评:本题考查了等边三角形的性质,等腰三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
下列各组的两项,不是同类项的是( )
| A、2x与x2 | ||
| B、-3a与3a | ||
| C、2m2n与-2nm2 | ||
D、12与
|
 如图,⊙A,⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )
如图,⊙A,⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )A、
| ||
B、
| ||
| C、π | ||
| D、π |
 已知数轴上的点A和点B之间的距离为32个单位长度,点A在原点的左边,距离原点5个单位长度,点B在原点的右边.
已知数轴上的点A和点B之间的距离为32个单位长度,点A在原点的左边,距离原点5个单位长度,点B在原点的右边.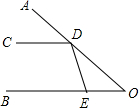 如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.
如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.