题目内容
7.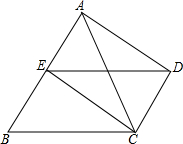 已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=$\frac{1}{2}$AB,请对△ABC添加一个条件:AB=2BC,使得四边形BCDE成为菱形.
已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=$\frac{1}{2}$AB,请对△ABC添加一个条件:AB=2BC,使得四边形BCDE成为菱形.
分析 先由已知条件得出CD=BE,证出四边形BCDE是平行四边形,再证出BE=BC,根据邻边相等的平行四边形是菱形可得四边形BCDE是菱形.
解答 解:添加一个条件:AB=2BC,可使得四边形BCDE成为菱形.理由如下:
∵DC=$\frac{1}{2}$AB,E为AB的中点,
∴CD=BE=AE.
又∵DC∥AB,
∴四边形BCDE是平行四边形,
∵AB=2BC,
∴BE=BC,
∴四边形BCDE是菱形.
故答案为:AB=2BC.
点评 本题考查了菱形的判定,平行四边形的判定;熟记平行四边形和菱形的判定方法是解决问题的关键.

练习册系列答案
相关题目
18. 如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )
如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )
 如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )
如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )| A. | 65° | B. | 115° | C. | 125° | D. | 135° |
17.关于x的不等式组$\left\{\begin{array}{l}{2x<3(x-3)}\\{\frac{x+2}{2}>x+a}\end{array}\right.$ 有四个整数解,则a的取值范围是( )
| A. | -6≤a≤-$\frac{11}{2}$ | B. | -6<a≤-$\frac{11}{2}$ | C. | -6<a<-$\frac{11}{2}$ | D. | -6≤a<-$\frac{11}{2}$ |
 如图,经过平移,将的顶点A移到了点D,请作出平移后图形.
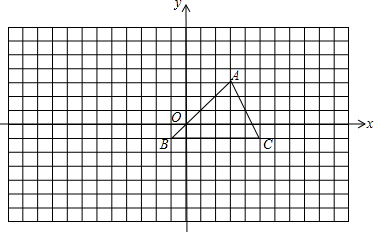
如图,经过平移,将的顶点A移到了点D,请作出平移后图形.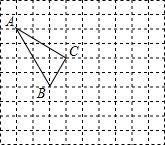 在如图所示的正方形网格中,每个小正方形的边长为1,如果格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).
在如图所示的正方形网格中,每个小正方形的边长为1,如果格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1). 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2016个等腰直角三角形的斜边长是21008.
如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2016个等腰直角三角形的斜边长是21008.