题目内容
5.先化简,再求值:$\frac{2x+4}{x-2}$÷(x+2)-$\frac{x^2-4}{x^2-4x+4}$,其中x=6.分析 首先将分式的分子与分母进行分解因式进而化简,再将x的值代入求出答案.
解答 解:$\frac{2x+4}{x-2}$÷(x+2)-$\frac{x^2-4}{x^2-4x+4}$
=$\frac{2(x+2)}{x-2}$×$\frac{1}{x+2}$-$\frac{(x+2)(x-2)}{(x-2)^{2}}$
=$\frac{2}{x-2}$-$\frac{x+2}{x-2}$
=$\frac{-x}{x-2}$,
将x=6代入上式可得:原式=$\frac{-6}{6-2}$=-$\frac{3}{2}$.
点评 此题主要考查了分式的化简求值,正确分解因式是解题关键.

练习册系列答案
相关题目
17.关于x的不等式组$\left\{\begin{array}{l}{2x<3(x-3)}\\{\frac{x+2}{2}>x+a}\end{array}\right.$ 有四个整数解,则a的取值范围是( )
| A. | -6≤a≤-$\frac{11}{2}$ | B. | -6<a≤-$\frac{11}{2}$ | C. | -6<a<-$\frac{11}{2}$ | D. | -6≤a<-$\frac{11}{2}$ |
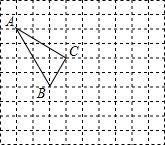 在如图所示的正方形网格中,每个小正方形的边长为1,如果格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).
在如图所示的正方形网格中,每个小正方形的边长为1,如果格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).