题目内容
2.计算:①-13-(-5)+2
②$-6×(-1\frac{2}{7})÷\frac{18}{5}$
③${({-3})^2}+8×({\frac{1}{2}-\frac{3}{4}})$
④$89\frac{24}{25}×(-5)$(用简便方法计算)
分析 ①先化简,再计算加减法;
②将除法变为乘法,再约分计算即可求解;
③按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的;
④运用乘法的分配律计算.
解答 解:①-13-(-5)+2
=-13+5+2
=-6;
②$-6×(-1\frac{2}{7})÷\frac{18}{5}$
=6×$\frac{9}{7}$×$\frac{5}{18}$
=$\frac{15}{7}$;
③${({-3})^2}+8×({\frac{1}{2}-\frac{3}{4}})$
=9+8×(-$\frac{1}{4}$)
=9-2
=7;
④$89\frac{24}{25}×(-5)$
=(90-$\frac{1}{25}$)×(-5)
=90×(-5)-$\frac{1}{25}$×(-5)
=-450+$\frac{1}{5}$
=$-449\frac{4}{5}$
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.

练习册系列答案
相关题目
13.绝对值等于5的数是( )
| A. | 5 | B. | -5 | C. | +5或-5 | D. | 5分之1 |
10.绝对值小于3.5的整数共有( )
| A. | 3个 | B. | 5个 | C. | 7个 | D. | 9个 |
7.王老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a=n2-1,b=2n,c=n2+1.
(2)猜想:以a,b,c为边的三角形是否为直角三角形?并证明你的猜想?
(3)观察下列勾股数32+42=52,52+122=132,72+242=252,92+402=412,分析其中的规律,写出第五组勾股数112+602=612.
| n | 2 | 3 | 4 | 5 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | … |
| b | 4 | 6 | 8 | 10 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(2)猜想:以a,b,c为边的三角形是否为直角三角形?并证明你的猜想?
(3)观察下列勾股数32+42=52,52+122=132,72+242=252,92+402=412,分析其中的规律,写出第五组勾股数112+602=612.
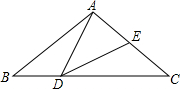 如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.