题目内容
2.(1)当a=2,b=1时时,分别求代数式①a2-2ab+b2 ②(a-b)2 的值.(2)当a=5,b=-3时,分别求代数式①a2-2ab+b2 ②(a-b)2的值.
(3)观察(1)(2)中代数式的值,a2-2ab+b2 与(a-b)2有何关系?
(4)利用你发现的规律,求135.72-2×135.7×35.7+35.72的值.
分析 (1)把a与b的值分别代入各式计算即可得到结果;
(2)把a与b的值分别代入各式计算即可得到结果;
(3)观察上面代数式的值,得出两数相等;
(4)利用得出的规律将原式变形,计算即可得到结果.
解答 解:(1)当a=2,b=1时,①a2-2ab+b2=4-4+1=1;②(a-b)2=1;
(2)当a=5,b=-3时,①a2-2ab+b2=25+30+9=64;②(a-b)2=64;
(3)可得a2-2ab+b2=(a-b)2;
(4)原式=(135.7-35.7)2=1002=10000.
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.九年级数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤70且x为整数)天的售价目与销量的相关信息如下表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于3250元?请直接写出结果.
| 时间x(天) | 1≤x≤40 | 40≤x≤70 |
| 售价(元/件) | x+45 | 85 |
| 每天销售(件) | 150-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于3250元?请直接写出结果.
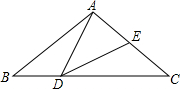 如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.