题目内容
2.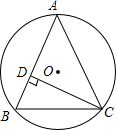 如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
分析 作直径BE,连接CE,作CF⊥BE于点F,则在直角△BCE中解直角三角形求得EC的长,然后根据勾股定理即可求得BC的长.
解答  解:作直径BE,连接CE,作CF⊥BE于点F.
解:作直径BE,连接CE,作CF⊥BE于点F.
∵CF⊥BE,CD⊥AB
又∵∠A=∠E,
∴∠ECF=∠ACD.
∵BE是直径,CF⊥BE,
∴∠BCE=90°,∠EBC=∠ECF=∠ACD,
∴sin∠EBC=sin∠ACD=$\frac{2}{3}$,
∴$\frac{CE}{BE}$=$\frac{2}{3}$,
∵BE=12,
∴CE=8,
∴BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=4$\sqrt{5}$
故答案是:4$\sqrt{5}$.
点评 本题考查了圆周角定理,以及三角函数的定义,勾股定理,正确作出辅助线是关键.

练习册系列答案
相关题目
12.甲.乙两车分别从A、B两地同时出发,相向而行,若快车甲的速度为60km/h,慢车乙的速度比快车甲慢4km/h,A、B两地相距80km,求两车出发到相遇所行时间.如果设xh后两车相遇,则根据题意列出方程( )
| A. | $\frac{x}{80}$+$\frac{x-4}{80}$=60 | B. | x(x-4)=80 | C. | 60x+(60-4)x=80 | D. | 60x+60(x-4)=80 |
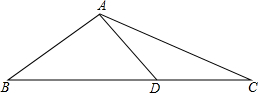 已知:在△ABC中,D为BC中点,且∠BAD=90°,tan∠B=$\frac{1}{3}$,求sin∠CAD、cos∠CAD、tan∠CAD的值.
已知:在△ABC中,D为BC中点,且∠BAD=90°,tan∠B=$\frac{1}{3}$,求sin∠CAD、cos∠CAD、tan∠CAD的值. 在正方形ABCD的对角线AC上取AE=AB,过E作AC的垂线交BC于F,求EF:AB的比值.
在正方形ABCD的对角线AC上取AE=AB,过E作AC的垂线交BC于F,求EF:AB的比值.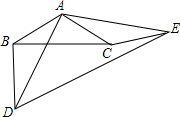 如图所示,△ABC,△ADE均是顶角为120°的等腰三角形,BC,DE分别是它们的底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?
如图所示,△ABC,△ADE均是顶角为120°的等腰三角形,BC,DE分别是它们的底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?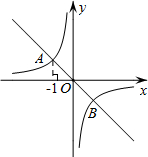 已知:如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=-$\frac{1}{x}$的图象交于A、B两点.
已知:如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=-$\frac{1}{x}$的图象交于A、B两点. 已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.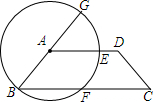 如图,在梯形ABCD中,AD∥BC,∠BAD=135°,以A为圆心,AB为半径作⊙A交AD,BC于E,F两点,并交BA延长线于G.求弧BF的度数.
如图,在梯形ABCD中,AD∥BC,∠BAD=135°,以A为圆心,AB为半径作⊙A交AD,BC于E,F两点,并交BA延长线于G.求弧BF的度数.