题目内容
17.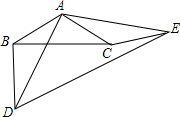 如图所示,△ABC,△ADE均是顶角为120°的等腰三角形,BC,DE分别是它们的底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?
如图所示,△ABC,△ADE均是顶角为120°的等腰三角形,BC,DE分别是它们的底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?
分析 由图可知,△ABD≌△ACE,所以两个三角形可以通过旋转相互得到.
解答 解:∵△ABC、△ADE均是顶角为120°的等腰三角形,
∴∠BAC=∠DAE=120°,
∴∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE,
∴△ABD与△ACE可通过旋转相互得到,
△ABD可以点A为旋转中心,逆时针旋转120°,使△ABD与△ACE重合.
点评 此题考查旋转的性质,三角形全等的判定,掌握等腰三角形的性质,能够熟练解决一些简单的旋转问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.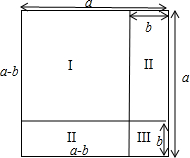 如图能验证的公式是 ( )
如图能验证的公式是 ( )
 如图能验证的公式是 ( )
如图能验证的公式是 ( )| A. | (a-b)(a+b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a-b)(a+b) |
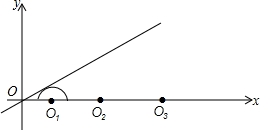 如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆
如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆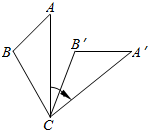 如图,将△ABC绕着点C顺时针旋转后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠B′CA′的度数是30°.
如图,将△ABC绕着点C顺时针旋转后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠B′CA′的度数是30°. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=7,BC=24,求tan∠ACD的值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=7,BC=24,求tan∠ACD的值.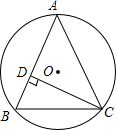 如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.