题目内容
14. 已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.(1)求证:四边形AFCE是菱形;
(2)若AB=5,BC=12,求AE的长.
分析 (1)由矩形的性质得出AO=OC,∠AOE=∠COF,由ASA证出△AOE≌△COF,得出OE=OF,证出四边形AFCE是平行四边形,再根据EF⊥AC即可得出四边形AFCE是菱形;
(2)设AE=CF=AF=x,则BF=12-x,在Rt△ABF中,由勾股定理得出方程,解方程即可.
解答 (1)证明:∵EF是AC的垂直平分线,
∴AO=OC,∠AOE=∠COF=90°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO.
在△AOE和△COF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}&{\;}\\{OA=OC}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF,
∵OA=OC,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,
∴平行四边形AFCE为菱形;
(2)解:∵四边形AFCE是菱形,
∴AE=AF=CF,
设AE=AF=CF=x,则BF=12-x,
在Rt△ABF中,由勾股定理得:
AB2+BF2=AF2,
即52+(12-x)2=x2,
解得:x=$\frac{169}{24}$,
∴AE=$\frac{169}{24}$.
点评 本题考查了勾股定理、矩形的性质、线段垂直平分线的性质、菱形的判定与性质、全等三角形的性质和判定、平行线的性质等知识点的综合运用;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
4.如图,下面是用棋子摆成的反写“T”字,按这样的规律摆下去,摆成第n个反写“T”字需要的棋子个数为( )


| A. | 3n+2 | B. | 2n+2 | C. | 3n+3 | D. | 2n+3 |
5.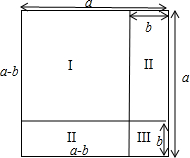 如图能验证的公式是 ( )
如图能验证的公式是 ( )
 如图能验证的公式是 ( )
如图能验证的公式是 ( )| A. | (a-b)(a+b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a-b)(a+b) |
19.有下列四个式子:①2x2+1=3x-4;②5a-b=3;③y2=1;④2t+1=7,其中是方程的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
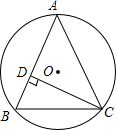 如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.