题目内容
13.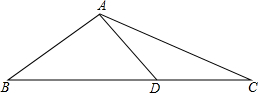 已知:在△ABC中,D为BC中点,且∠BAD=90°,tan∠B=$\frac{1}{3}$,求sin∠CAD、cos∠CAD、tan∠CAD的值.
已知:在△ABC中,D为BC中点,且∠BAD=90°,tan∠B=$\frac{1}{3}$,求sin∠CAD、cos∠CAD、tan∠CAD的值.
分析 延长AD到E,使DE=AD,连接CE,证得△ABD≌△CDE,得到∠E=∠BAD=90°,CE=AB,由于tan∠B=$\frac{1}{3}$,设CE=AB=3k,AD=DE=k,则AE=2k,根据勾股定理求得AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{13}$k,然后根据三角函数的定义即可得到结论.
解答  解:延长AD到E,使DE=AD,连接CE,
解:延长AD到E,使DE=AD,连接CE,
∵D为BC中点,
∴BD=CD,
在△ABD与△CDE中,$\left\{\begin{array}{l}{AD=DE}\\{∠ADB=∠CDE}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△CDE,
∴∠E=∠BAD=90°,CE=AB,
∵tan∠B=$\frac{1}{3}$,
∴设CE=AB=3k,AD=DE=k,
则AE=2k,
∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{13}$k,
∴sin∠CAD=$\frac{CE}{AC}$=$\frac{3k}{\sqrt{13}k}$=$\frac{3\sqrt{13}}{13}$,
cos∠CAD=$\frac{AE}{AC}$=$\frac{2k}{\sqrt{13}k}$=$\frac{2\sqrt{13}}{13}$,
tan∠CAD=$\frac{CE}{AE}$=$\frac{3k}{2k}$=$\frac{3}{2}$.
点评 本题考查了解直角三角形,线段中点的定义,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
4.如图,下面是用棋子摆成的反写“T”字,按这样的规律摆下去,摆成第n个反写“T”字需要的棋子个数为( )


| A. | 3n+2 | B. | 2n+2 | C. | 3n+3 | D. | 2n+3 |
1.下列方程是一元二次方程的是( )
| A. | 3x+$\frac{1}{x}$=4 | B. | 2x(x-1)=2x2+3 | C. | x2-2=0 | D. | x+2y=1 |
5.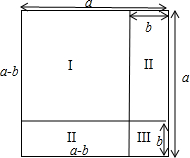 如图能验证的公式是 ( )
如图能验证的公式是 ( )
 如图能验证的公式是 ( )
如图能验证的公式是 ( )| A. | (a-b)(a+b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a-b)(a+b) |
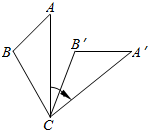 如图,将△ABC绕着点C顺时针旋转后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠B′CA′的度数是30°.
如图,将△ABC绕着点C顺时针旋转后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠B′CA′的度数是30°.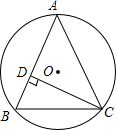 如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.