题目内容
12.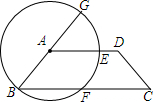 如图,在梯形ABCD中,AD∥BC,∠BAD=135°,以A为圆心,AB为半径作⊙A交AD,BC于E,F两点,并交BA延长线于G.求弧BF的度数.
如图,在梯形ABCD中,AD∥BC,∠BAD=135°,以A为圆心,AB为半径作⊙A交AD,BC于E,F两点,并交BA延长线于G.求弧BF的度数.
分析 连接AF,由平行线的性质得出∠B=45°,由等腰三角形的性质得出∠AFB=∠B=45°,由三角形内角和定理得出∠BAF=90°,即可得出$\widehat{BF}$的度数.
解答 解:连接AF,如图所示:
∵AD∥BC,∠BAD=135°,
∴∠B+∠BAD=180°,
∴∠B=45°,
∵AF=AB,
∴∠AFB=∠B=45°,
∴∠BAF=180°-45°-45°=90°,
∴$\widehat{BF}$的度数为90°.
点评 本题考查了梯形的性质、等腰三角形的性质、圆心角、弧、弦的关系;熟练掌握梯形的性质,由等腰三角形的性质求出圆心角的度数是解决问题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
5.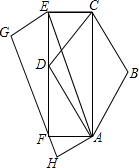 如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
 如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )| A. | S1>S2>S3 | B. | S1<S2<S3 | C. | S1=S2=S3 | D. | S1>S2>S3 |
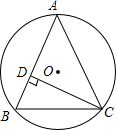 如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.
如图,△ABC内接于⊙O,半径为6,CD⊥AB于点D,sin∠ACD=$\frac{2}{3}$,则BC的长为4$\sqrt{5}$.