题目内容
18.某小区为了绿化环境,计划分两次购进A、B两种花草(两次购进的A、B两种花草价格均分别相同).购买数量和费用如表:| A | B | 费用(元) | |
| 第一次 | 30 | 15 | 675 |
| 第二次 | 12 | 5 | 265 |
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,设购买A种花草x棵,购买费用为y元;
①写出y与x的函数关系式;
②请你给出一种费用最省的方案,并求出该方案所需费用.
分析 (1)设A种花草每棵的价格m元,B种花草每棵的价格n元,根据第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵,共花费265元;列出方程组,即可解答;
(2)①根据:总费用=A种花草的购买总费用+B种花草的购买总费用,可列出y关于x的函数解析式;
②由“B种花草的数量<2×A种花草的数量”列不等式可得x的范围,根据一次函数性质可得y的最值情况.
解答 解:(1)设A种花草每棵的价格m元,B种花草每棵的价格n元,根据题意,
得:$\left\{\begin{array}{l}{30m+15n=675}\\{12m+5n=265}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=20}\\{n=5}\end{array}\right.$,
答:A种花草每棵的价格是20元,B种花草每棵的价格是5元.
(2)①设购买A种花草x棵,则购买B种花草(31-x)棵,购买费用为y元,
则:y=20x+5(31-x)=15x+155;
②∵B种花草的数量少于A种花草的数量的2倍,
∴31-x<2x,
解得:x>$\frac{31}{3}$,
∵x是正整数,
∴x最小值=11,
∵y=15x+155中,y随x的减小而减小,
∴当x=11时,y取得最小值,y最小值=15×11+155=320(元).
答:购进A种花草的数量为11棵、B种20棵,费用最省;最省费用是320元.
点评 本题考查了列二元一次方程组、一元一次不等式解实际问题的运用、一次函数的解析式的运用、一次函数的性质的运用,解答时根据总费用=两种花草的费用之和建立函数关系式,根据自变量的取值范围结合一次函数性质求得函数的最值是关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
9.下列方程中,无实数解的是( )
| A. | 2+x=0 | B. | 2-x=0 | C. | 2x=0 | D. | $\frac{2}{x}$=0 |
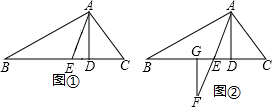
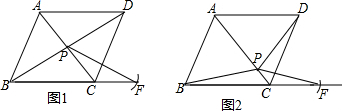
 如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$.
如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$. 如图,四边形ABCD内接于⊙O,∠A=100°,⊙O的半径=2,则劣弧$\widehat{BD}$的长=$\frac{16π}{9}$.
如图,四边形ABCD内接于⊙O,∠A=100°,⊙O的半径=2,则劣弧$\widehat{BD}$的长=$\frac{16π}{9}$.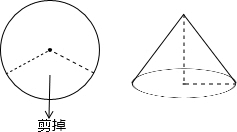 如图,若将半径为6cm的圆形纸片剪去$\frac{1}{3}$,剩下的部分围成一个圆锥的侧面,则围成圆锥的全面积为40π(cm2).
如图,若将半径为6cm的圆形纸片剪去$\frac{1}{3}$,剩下的部分围成一个圆锥的侧面,则围成圆锥的全面积为40π(cm2).