题目内容
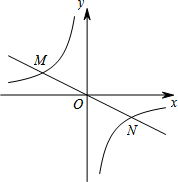 如图,正比例函数y=-
如图,正比例函数y=-| 1 |
| 2 |
| k |
| x |
(1)求反比例函数的表达式;
(2)点P为y轴上的一点,当∠MPN为直角时,直接写出点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把M(-2,m)代入函数式y=-
x中,求得m的值,从而求得M的坐标,代入y=
可求出函数解析式;
(2)根据M的坐标求得N的坐标,设P(0,m),根据勾股定理列出关于m的方程,解方程即可求得m进而求得P的坐标.
| 1 |
| 2 |
| k |
| x |
(2)根据M的坐标求得N的坐标,设P(0,m),根据勾股定理列出关于m的方程,解方程即可求得m进而求得P的坐标.
解答:解:(1)∵点M(-2,m)在正比例函数y=-
x的图象上,
∴m=-
×(-2)=1,
∴M(-2,1),
∵反比例函数y=
的图象经过点M(-2,1),
∴k=-2×1=-2.
∴反比例函数的解析式为y=-
.
(2)∵正比例函数y=-
x的图象与反比例函数y=
的图象分别交于M,N两点,点M(-2,1),
∴N(2,-1),
∵点P为y轴上的一点,
∴设P(0,m),
∵∠MPN为直角,
∴△MPN是直角三角形,
∴(0+2)2+(m-1)2+(0-2)2+(m+1)2=(2+2)2+(-1-1)2,
解得m=±
∴点P的坐标为(0,
)或(0,-
).
| 1 |
| 2 |
∴m=-
| 1 |
| 2 |
∴M(-2,1),
∵反比例函数y=
| k |
| x |
∴k=-2×1=-2.
∴反比例函数的解析式为y=-
| 2 |
| x |
(2)∵正比例函数y=-
| 1 |
| 2 |
| k |
| x |
∴N(2,-1),
∵点P为y轴上的一点,
∴设P(0,m),
∵∠MPN为直角,
∴△MPN是直角三角形,
∴(0+2)2+(m-1)2+(0-2)2+(m+1)2=(2+2)2+(-1-1)2,
解得m=±
| 5 |
∴点P的坐标为(0,
| 5 |
| 5 |
点评:考查了反比例函数与一次函数的交点问题,本题利用了待定系数法求函数解析式以及利用中心对称求两个函数的交点,两点之间距离公式、勾股定理等知识.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
“二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据对这句话的理解,解决下面问题:若m,n(m<n)是关于x的方程2-(x-a)(x-b)=0的两根,且a<b,则a,b,m,n的大小关系是( )
| A、a<m<n<b |
| B、a<m<b<n |
| C、m<a<b<n |
| D、m<a<n<b |
 如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )
如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )A、
| ||
B、
| ||
C、
| ||
| D、300πcm2 |
已知某种商品的进价为1600元,新年期间,商场为了促销,对该商品按标价的8折出售,仍可获利160元,则该商品的标价应为( )
| A、2400元 |
| B、2200元 |
| C、2000元 |
| D、1800元 |
把一个长方形划分成三个全等的长方形,若要使每一个小长方形与原长方形相似,则原长方形的长a与宽b的关系是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.
如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.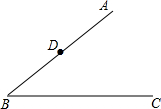 如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题:
如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题: