题目内容

1．计算：
（1）$\frac{12}{{m}^{2}-9}$-$\frac{2}{m-3}$         
（2）（$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$-$\frac{x-2}{x+2}$）÷$\frac{x}{x-2}$
（3）$\frac{{x}^{2}}{x-1}$-x-1             
（4）（1+$\frac{1}{x-1}$）÷$\frac{x}{{x}^{2}-1}$．

分析 （1）原式通分并利用同分母分式的减法法则计算，约分即可得到结果；
（2）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果；
（3）原式通分并利用同分母分式的减法法则计算即可得到结果；
（4）原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分即可得到结果．

解答 解：（1）原式=$\frac{12-2（m+3）}{（m+3）（m-3）}$=$\frac{-2（m-3）}{（m+3）（m-3）}$=-$\frac{2}{m+3}$；
（2）原式=[$\frac{（x+2）（x-2）}{（x-2）^{2}}$-$\frac{x-2}{x+2}$]•$\frac{x-2}{x}$=$\frac{（x+2）^{2}-（x-2）^{2}}{（x+2）（x-2）}$•$\frac{x-2}{x}$=$\frac{8x}{（x+2）（x-2）}$•$\frac{x-2}{x}$=$\frac{8}{x+2}$；
（3）原式=$\frac{{x}^{2}-（x+1）（x-1）}{x-1}$=$\frac{1}{x-1}$；
（4）原式=$\frac{x}{x-1}$•$\frac{（x+1）（x-1）}{x}$=x+1．

点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
11．已知x+y=-4，xy=-12，则$\frac{x+1}{y+1}+\frac{y+1}{x+1}$=-$\frac{34}{15}$．
12．解方程：
（1）$\frac{1}{x-2}=\frac{1-x}{2-x}$
（2）$\frac{7-9x}{2-3x}-\frac{4x-5}{2-3x}=1$
（3）$\frac{5}{{{x^2}+3x}}-\frac{1}{{{x^2}-x}}=0$
（4）$\frac{2}{1+x}-\frac{3}{1-x}=\frac{6}{{{x^2}-1}}$．
9．计算：
（1）${（\sqrt{5}+1）^0}-\sqrt{12}+|{-\sqrt{3}}|$
（2）$（\sqrt{27}+\sqrt{20}）+（\sqrt{75}-\sqrt{5}）$
（3）$（\sqrt{2}+3）（\sqrt{2}-5）$
（4）$（4\sqrt{2}-3\sqrt{6}）÷2\sqrt{2}$
（5）$（\sqrt{5}+\sqrt{3}）（\sqrt{5}-\sqrt{3}）$
（6）${（\sqrt{3}-\sqrt{2}）^2}$．
16．关于x的方程$\frac{2ax+3}{a-x}$=$\frac{5}{4}$的根为x=2，则a应取值（　　）
A．1B．3C．-2D．-3
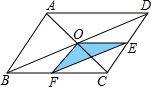6．如图，O是平行四边形ABCD对角线的交点，OE∥AD交CD于E，OF∥AB于F，那么S△OEF：S平行四边形ABCD=1：8．
13．（1）$\sqrt{8}$+2$\sqrt{3}$-（$\sqrt{27}$-$\sqrt{2}$）；      
（2）2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{2}$；
（3）（$\sqrt{2}$-$\sqrt{3}$）2+2$\sqrt{\frac{1}{3}}$×3$\sqrt{2}$；   
（4）（2-$\sqrt{3}$）2013•（2+$\sqrt{3}$）2014-2|-$\frac{\sqrt{3}}{2}$|-（-$\sqrt{3}$）
10．如图，∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，从左起第1个等边三角形的边长记为a1，第2个等边三角形的边长记为a2，以此类推．若OA1=1，则a2015=22014．
11．已知：如图，△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD．
（1）求证：AP=PD；
（2）若⊙O的半径为5，AF=7，求$\frac{AD}{BD}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网