Question

8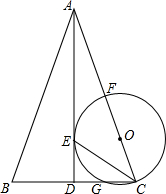．如图，△ABC中，AB=AC，AD⊥BC，AD=4，CE平分∠ACB交AD于点E．以线段CE为弦作⊙O，且圆心O落在AC上，⊙O交AC于点F，交BC于点G．
（1）求证：AD与⊙O的相切；
（2）若点G为CD的中点，求⊙O的半径；
（3）判断点E能否为AD的中点，若能则求出BC的长，若不能请说明理由．

Answer 1

分析 （1）根据等腰三角形的性质得到∠OEC=∠OCE，由角平分线的定义得到∠OCE=∠DCE，等量代换得到∠OEC=∠DCE，得到OE∥BC，根据平行线的性质得到OE⊥AD，即可得到结论；
（2）由等腰三角形的性质得到∠OGC=∠OCG，∠B=∠ACB，推出OG∥AB，根据平行线分线段成比例定理得到$\frac{CG}{BC}=\frac{OC}{AC}$，得到$\frac{OC}{AC}=\frac{1}{4}$，根据相似三角形的性质得到$\frac{OH}{AD}=\frac{OC}{AC}$=$\frac{1}{4}$，得到DE=OH=1，然后根据相似三角形的性质即可得到结论．
（3）假设点E能为AD的中点，根据三角形的中位线的性质得到AO=OC，推出OE=$\frac{1}{2}AC$=$\frac{1}{2}$CD，得到AB+AC=BC，即△ABC不存在，于是得到结论．

解答 （1）证明：连接OE，
∵OE=OC，
∴∠OEC=∠OCE，
∵CE平分∠ACB，
∴∠OCE=∠DCE，
∴∠OEC=∠DCE，
∴OE∥BC，
∵AD⊥BC，
∴OE⊥AD，
∴AD与⊙O的相切；

（2）连接OG，过O作OH⊥CD于H，
∴OH∥AD，
∵OG=OC，
∴∠OGC=∠OCG，
∵AB=AC，
∴∠B=∠ACB，
∴∠B=∠OGC，
∴OG∥AB，
∵$\frac{CG}{BC}=\frac{OC}{AC}$，
∵点G为CD的中点，
∴CG=$\frac{1}{2}$CD=$\frac{1}{4}$BC，
∴$\frac{OC}{AC}=\frac{1}{4}$，
∴OH∥AD，
∴△COH∽△CAD，
∴$\frac{OH}{AD}=\frac{OC}{AC}$=$\frac{1}{4}$，
∴OH=1，
∴DE=OH=1，
∵AD与⊙O的相切，
∴DE²=DG•CD=2DG²，
∴DG=$\frac{\sqrt{2}}{2}$，
∴CD=$\sqrt{2}$，
∵OE∥CD，
∴△AOE∽△ADC，
∴$\frac{AE}{AD}=\frac{OE}{CD}$，
∴OE=$\frac{3\sqrt{2}}{4}$，
∴⊙O的半径是$\frac{3\sqrt{2}}{4}$；

（3）点E不能为AD的中点，
假设点E能为AD的中点，
∵OE∥CD，
∴AO=OC，
∴AC为⊙O的直径，OE=$\frac{1}{2}AC$=$\frac{1}{2}$CD，
∵CD=BD，AB=AC，
∴AB+AC=BC，即△ABC不存在，
故点E不能为AD的中点．

点评 本题考查了切线的判定和性质，等腰三角形的性质，相似三角形的判定和性质，平行线的判定和性质，三角形的中位线的性质，切割线定理，连接OG，过O作OH⊥CD于H构造相似三角形是解题的关键．