题目内容
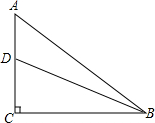
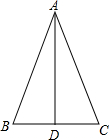 如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.
如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.(1)求AC的长.
(2)求AC边上的高.
考点:勾股定理的逆定理,勾股定理
专题:
分析:(1)先根据勾股定理的逆定理判断出△ABD的形状,再根据点D为BC边上的中点即可得出△ABC是等腰三角形,故可得出AC的长;
(2)设AC边上的高为h,再根据三角形的面积公式即可得出结论.
(2)设AC边上的高为h,再根据三角形的面积公式即可得出结论.
解答:解:(1)∵△ABD中,AB=13,AD=12,BD=5,52+122=132,
∴△ABD是直角三角形,即AD⊥BC.
∵点D为BC边上的中点,
∴△ABC是等腰三角形,
∴AC=AB=13;
(2)设AC边上的高为h,
∵由(1)知△ABC是等腰三角形,
∴CD=BD=5,
∴AD•CD=AC•h,
∴h=
=
=
.
∴△ABD是直角三角形,即AD⊥BC.
∵点D为BC边上的中点,
∴△ABC是等腰三角形,
∴AC=AB=13;
(2)设AC边上的高为h,
∵由(1)知△ABC是等腰三角形,
∴CD=BD=5,
∴AD•CD=AC•h,
∴h=
| AD•CD |
| AC |
| 12×5 |
| 13 |
| 60 |
| 13 |
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 如图,∠1=∠2,∠3=∠4.求证:CE=DE.
如图,∠1=∠2,∠3=∠4.求证:CE=DE.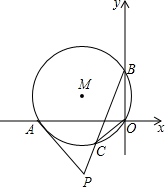 如图,在直角坐标系中,⊙M经过原点O,与x轴交与点A,与y轴交与点B,点C是劣弧OA的中点,切线AP与BC的延长线交与点P,已知点A的坐标为(-3,0),OC的长是方程x2-2
如图,在直角坐标系中,⊙M经过原点O,与x轴交与点A,与y轴交与点B,点C是劣弧OA的中点,切线AP与BC的延长线交与点P,已知点A的坐标为(-3,0),OC的长是方程x2-2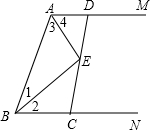 如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,∠MAB、∠NBA的平分线交于E.
如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,∠MAB、∠NBA的平分线交于E.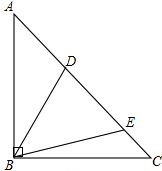 如图,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE=
如图,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE=
 如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=
如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=