题目内容
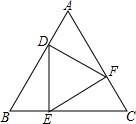 如图所示,在等边△ABC中,D、E、F分别是AB、BC、AC、上的点,DE⊥BC,EF⊥AC,FD⊥AB,BE=3,则△ABC的周长为
如图所示,在等边△ABC中,D、E、F分别是AB、BC、AC、上的点,DE⊥BC,EF⊥AC,FD⊥AB,BE=3,则△ABC的周长为考点:全等三角形的判定与性质,含30度角的直角三角形
专题:
分析:由△ABC是等边三角形和DE⊥BC,EF⊥AC,FD⊥AB,求出∠BDE=∠FEC=∠AFD=30°,推出∠DEF=∠DFE=∠EDF=60°,推出DF=DE=EF,即可得出等边三角形DEF,根据全等三角形性质推出三个三角形全等即可.求出AB=3BE,进一步得出答案即可.
解答:解:∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠C=∠A=60°,
∵DE⊥BC、EF⊥AC、FD⊥AB,
∴∠DEB=∠EFC=∠FDA=90°,
∴∠BDE=∠FEC=∠AFD=30°,
∴∠DEF=∠DFE=∠EDF=180°-90°-30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形,
在△ADF、△BED、△CFE中,
,
∴△ADF≌△BED≌△CFE(AAS),
∴AD=BE=CF,
∵∠DEB=90°,∠BDE=30°,
∴BD=2BE,
∴AB=3BE=9,
∴△ABC的周长为9×3=27.
故答案为:27.
∴AB=AC=BC,∠B=∠C=∠A=60°,
∵DE⊥BC、EF⊥AC、FD⊥AB,

∴∠DEB=∠EFC=∠FDA=90°,
∴∠BDE=∠FEC=∠AFD=30°,
∴∠DEF=∠DFE=∠EDF=180°-90°-30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形,
在△ADF、△BED、△CFE中,
|
∴△ADF≌△BED≌△CFE(AAS),
∴AD=BE=CF,
∵∠DEB=90°,∠BDE=30°,
∴BD=2BE,
∴AB=3BE=9,
∴△ABC的周长为9×3=27.
故答案为:27.
点评:此题考查了等边三角形性质,含30度角的直角三角形性质,全等三角形的性质和判定的应用,主要锻炼学生的推理能力.

练习册系列答案
相关题目
把下列各数填入表示它所在的数集的大括号:
3π,-2,-
,3.020020002…,0,
,-(-3),0.333
整数集合:{ …}
分数集合:{ …}
负有理数集合:{ …}
无理数集合:{ …}.
3π,-2,-
| 1 |
| 2 |
| 22 |
| 7 |
整数集合:{ …}
分数集合:{ …}
负有理数集合:{ …}
无理数集合:{ …}.
(m+n)(m+n-2)-8=0,则m+n的值是( )
| A、4 | B、-2 |
| C、4或-2 | D、-4或2 |
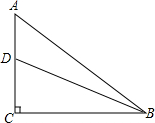 如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=
如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA= 如图,已知△ABC中,AB=AC,AB边上的垂直平分线DE交AC于点E,D为垂足,若∠ABE:∠EBC=2:1,则∠A=
如图,已知△ABC中,AB=AC,AB边上的垂直平分线DE交AC于点E,D为垂足,若∠ABE:∠EBC=2:1,则∠A=