题目内容
 如图,OC平分∠AOB,∠AOC=20°,P为OC上一点,PD=PE,OD≠OE,∠OPE=110°,则∠ODP=
如图,OC平分∠AOB,∠AOC=20°,P为OC上一点,PD=PE,OD≠OE,∠OPE=110°,则∠ODP=考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:过点P作PF⊥OA于F,作PG⊥OB于G,根据角平分线上的点到角的两边距离相等可得PF=PG,再利用“HL”证明Rt△OPF和Rt△OPG全等,根据全等三角形对应角相等可得∠PEG=∠PDF,根据角平分线的定义可得∠BOC=∠AOC,再利用三角形的内角和定理求出∠PEG,然后根据平角的定义列式计算即可得解.
解答: 解:如图,过点P作PF⊥OA于F,作PG⊥OB于G,
解:如图,过点P作PF⊥OA于F,作PG⊥OB于G,
∵OC平分∠AOB,
∴PF=PG,
在Rt△OPF和Rt△OPG中,
,
∴Rt△OPF≌Rt△OPG(HL),
∴∠PEG=∠PDF,
∵OC平分∠AOB,∠AOC=20°,
∴∠BOC=∠AOC=20°,
∵∠OPE=110°,
∴∠PEG=180°-20°-110°=50°,
∴∠PDF=∠PEG=50°,
∴∠ODP=180°-∠PDF=180°-50°=130°.
故答案为:130.
 解:如图,过点P作PF⊥OA于F,作PG⊥OB于G,
解:如图,过点P作PF⊥OA于F,作PG⊥OB于G,∵OC平分∠AOB,
∴PF=PG,
在Rt△OPF和Rt△OPG中,
|
∴Rt△OPF≌Rt△OPG(HL),
∴∠PEG=∠PDF,
∵OC平分∠AOB,∠AOC=20°,
∴∠BOC=∠AOC=20°,
∵∠OPE=110°,
∴∠PEG=180°-20°-110°=50°,
∴∠PDF=∠PEG=50°,
∴∠ODP=180°-∠PDF=180°-50°=130°.
故答案为:130.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列运算结果正确的是( )
| A、x3+x3=x4 |
| B、(x3)2=x5 |
| C、x3+x4=x2 |
| D、x•x3=x4 |
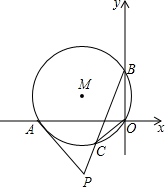 如图,在直角坐标系中,⊙M经过原点O,与x轴交与点A,与y轴交与点B,点C是劣弧OA的中点,切线AP与BC的延长线交与点P,已知点A的坐标为(-3,0),OC的长是方程x2-2
如图,在直角坐标系中,⊙M经过原点O,与x轴交与点A,与y轴交与点B,点C是劣弧OA的中点,切线AP与BC的延长线交与点P,已知点A的坐标为(-3,0),OC的长是方程x2-2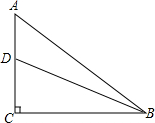 如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=
如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA= 如图,在△ABC中,∠B、∠C的平分线相交于点O,OB=OC,求证:△ABC是等腰三角形.
如图,在△ABC中,∠B、∠C的平分线相交于点O,OB=OC,求证:△ABC是等腰三角形.