题目内容
 如图,直线y=-x+2
如图,直线y=-x+2| 3 |
| k |
| x |
考点:反比例函数综合题
专题:
分析:分别过P、P1作x、y轴垂线,垂足分别为C、D点.设P1点坐标为(m,
),根据旋转的性质得到P点坐标为:(
,-m),根据三角函数得到tan30°=-
=
①,根据直线解析式得到m=-
+2
+2②,两者联立解方程组求得k的值.
| k |
| m |
| k |
| m |
| m | ||
|
| ||
| 3 |
| k |
| m |
| 3 |
解答: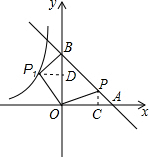 解:分别过P、P1作x、y轴垂线,垂足分别为C、D点,
解:分别过P、P1作x、y轴垂线,垂足分别为C、D点,
设P1点坐标为(m,
),
∵OP⊥OP1,OP=OP1,
∴∠P1OD=∠POC=30°,
∴OC=
,PC=-m,
∴P点坐标为:(
,-m),
由tan30°=-
=
①,
∴k=-
m2,
又∵P点在直线AB上,
∴-将k=-
m2代入②化简得:m=-2,
∴k=-4
.
故k的值是-4
.
 解:分别过P、P1作x、y轴垂线,垂足分别为C、D点,
解:分别过P、P1作x、y轴垂线,垂足分别为C、D点,设P1点坐标为(m,
| k |
| m |
∵OP⊥OP1,OP=OP1,
∴∠P1OD=∠POC=30°,
∴OC=
| k |
| m |
∴P点坐标为:(
| k |
| m |
由tan30°=-
| m | ||
|
| ||
| 3 |
∴k=-
| 3 |
又∵P点在直线AB上,
∴-将k=-
| 3 |
∴k=-4
| 3 |
故k的值是-4
| 3 |
点评:此题考查了反比例函数综合题,涉及的知识有:利用待定系数法求反比例函数解析式,旋转的性质,三角函数,一次函数,利用了数形结合及方程思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,∠1=∠2,∠3=∠4.求证:CE=DE.
如图,∠1=∠2,∠3=∠4.求证:CE=DE.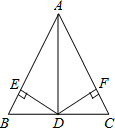 如图,AD是BC的中垂线,DE⊥AB,DF⊥AC,垂足分别为E,F,说明下列结论的理由:
如图,AD是BC的中垂线,DE⊥AB,DF⊥AC,垂足分别为E,F,说明下列结论的理由: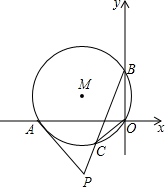 如图,在直角坐标系中,⊙M经过原点O,与x轴交与点A,与y轴交与点B,点C是劣弧OA的中点,切线AP与BC的延长线交与点P,已知点A的坐标为(-3,0),OC的长是方程x2-2
如图,在直角坐标系中,⊙M经过原点O,与x轴交与点A,与y轴交与点B,点C是劣弧OA的中点,切线AP与BC的延长线交与点P,已知点A的坐标为(-3,0),OC的长是方程x2-2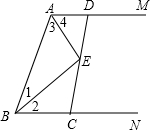 如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,∠MAB、∠NBA的平分线交于E.
如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,∠MAB、∠NBA的平分线交于E.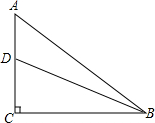 如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=
如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=