��Ŀ����
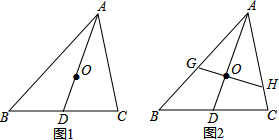
3����֪Rt��ABC�У�AC=BC����C=90�㣬DΪAB�е㣬��EDF=90�㣬�ҡ�EDF��D����ת���������߷ֱ�AC��CB�������ǵ��ӳ��ߣ���E��F����1������EDF��D����ת��DE��ACʱ��ͼ1������֤��${S_{��DEF}}+{S_{��CEF}}=\frac{1}{2}{S_{��ABC}}$��
��2������EDF��D����ת��DE��AC����ֱ��
�ٵ�������AC��BC�ཻʱ������ͼ2�������������Ƿ�������������������֤����������������˵�����ɣ�
�ڵ�������AC��BC���ӳ����ཻʱ������ͼ3�������������Ƿ�������������������֤����������������˵��S��DEF��S��CEF��S��ABC֮��Ĺ�ϵ��������֤����ֱ�ӻشɣ�
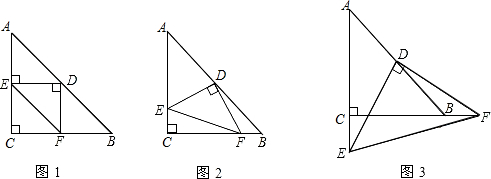
���� ��1������EDF��D����ת��DE��ACʱ���ı���CEDF�������Σ��߳���AC��һ�룬���ɵó����ۣ�
��2����������֤����CDE�ա�BDF�����ɵó����ۣ�
��3����������ͬ��2���ã���DEC�ա�DBF���ó�S��DEF=S�����DBFEC=S��CFE+S��DBC=S��CFE+$\frac{1}{2}$S��ABC��
��� �⣺��1������EDF��D����ת��DE��ACʱ���ı���CEDF�������Σ����ABC�ı߳�AC=BC=a����������CEDF�ı߳�Ϊ$\frac{1}{2}$a
��${S_{��ABC}}=\frac{1}{2}{a^2}$��������CEDF�����${S_{CEDF}}={��\frac{1}{2}a��^2}=\frac{1}{4}{a^2}$
��${S_{��DEF}}+{S_{��CEF}}=\frac{1}{2}{S_{��ABC}}$��
��2���������۳������������£�����CD����ͼ2 ��ʾ��
��ʾ��
��AC=BC����ACB=90�㣬DΪAB�е㣬
���B=45�㣬��DCE=$\frac{1}{2}$��ACB=45�㣬CD��AB��CD=$\frac{1}{2}$AB=BD��
���DCE=��B����CDB=90�㣬
�ߡ�EDF=90�㣬
���1=��2��
�ڡ�CDE�͡�BDF�У�$\left\{\begin{array}{l}{��1=��2}&{\;}\\{CD=BD}&{\;}\\{��DCE=��B}&{\;}\end{array}\right.$��
���CDE�ա�BDF��ASA����
��S��DEF+S��CEF=S��ADE+S��BDF=$\frac{1}{2}$S��ABC��
��3����������${S_{��DEF}}-{S_{��CEF}}=\frac{1}{2}{S_{��ABC}}$���������£�����CD����ͼ3��ʾ��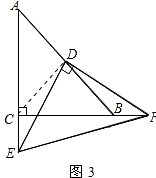
ͬ��2���ã���DEC�ա�DBF����DCE=��DBF=135��
��S��DEF=S�����DBFEC��
=S��CFE+S��DBC��
=S��CFE+$\frac{1}{2}$S��ABC��
��S��DEF-S��CFE=$\frac{1}{2}$S��ABC��
��S��DEF��S��CEF��S��ABC�Ĺ�ϵ�ǣ�S��DEF-S��CEF=$\frac{1}{2}$S��ABC��
���� ���⿼����ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ�ͼ���������֤��������ȫ���ǽ������Ĺؼ���

 ��ͼ����һ�����μ�����������һ�߿�ǽ��ǽ��18�ף����������������Χ�ɣ�����ʵ��ܳ�Ϊ35�ף���ǽƽ�еı�����1�����ţ����������������ɣ��������������Ϊ160ƽ���ף�����ǽ��ֱ�ı߳�Ϊ��������
��ͼ����һ�����μ�����������һ�߿�ǽ��ǽ��18�ף����������������Χ�ɣ�����ʵ��ܳ�Ϊ35�ף���ǽƽ�еı�����1�����ţ����������������ɣ��������������Ϊ160ƽ���ף�����ǽ��ֱ�ı߳�Ϊ��������| A�� | 7.5�� | B�� | 8�� | C�� | 10�� | D�� | 10��8�� |
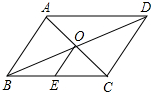 ��ͼ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E�DZ�BC���е㣬AB=4����OE�ij�Ϊ��������
��ͼ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E�DZ�BC���е㣬AB=4����OE�ij�Ϊ��������| A�� | $\sqrt{2}$ | B�� | 1 | C�� | $\frac{1}{2}$ | D�� | 2 |
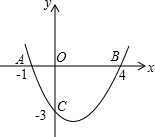 ��ͼ����֪���κ���y=ax2+bx+c��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�C��
��ͼ����֪���κ���y=ax2+bx+c��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�C�� ��֪��1=��2��AC=BD��E��F��A��B��ͬһֱ���ϣ��ʡ�3=��4��
��֪��1=��2��AC=BD��E��F��A��B��ͬһֱ���ϣ��ʡ�3=��4��