题目内容
5．计算：$\sqrt{b}$+$\sqrt{{a}^{3}b}$-（$\sqrt{{b}^{3}}$+$\sqrt{\frac{1}{ab}}$）分析 先去括号，再把各根式化为最减二次根式，合并同类项即可．
解答 解：原式=$\sqrt{b}$+a$\sqrt{ab}$-b$\sqrt{b}$-$\frac{\sqrt{ab}}{ab}$
=（1-b）$\sqrt{b}$+（a-$\frac{1}{ab}$）$\sqrt{ab}$．
点评 本题考查的是二次根式的加减法，熟知二次根式相加减，先把各个二次根式化成最简二次根式，再把被开方数相同的二次根式进行合并，合并方法为系数相加减，根式不变是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
相关题目
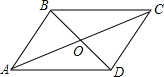如图，?ABCD周长为100cm，AC与BD交于O，△OAB的周长与△OBC的周长的和为122cm，AC：BD=5：4，求AC与BD的长．
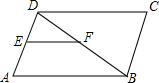如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为7．
10．
如图，在边长为12的正方形ABCD中，有一个小正方形EFGH，其中E、F分别在AB、BC上，FG在Rt△DCF上，若BF=3，则BE的长为（ ）
如图，在边长为12的正方形ABCD中，有一个小正方形EFGH，其中E、F分别在AB、BC上，FG在Rt△DCF上，若BF=3，则BE的长为（ ）| A． | 1 | B． | $\frac{5}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{9}{4}$ |
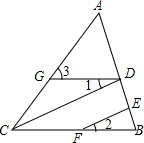填写推理理由：