题目内容
20.计算:(1)$\sqrt{8}+\sqrt{2}(1+\sqrt{2})$;
(2)($\sqrt{72}-2\sqrt{50}$)$÷\sqrt{2}$;
(3)($\sqrt{7}+1$)($\sqrt{7}-2$);
(4)(5$\sqrt{2}-2\sqrt{5}$)(2$\sqrt{2}$+5$\sqrt{3}$).
分析 (1)化简$\sqrt{8}$同时用乘法分配律去括号,再合并同类二次根式;
(2)直接计算除法,再化简二次根式即可;
(3)运用乘法分配律展开,再合并同类二次根式即可;
(4)运用乘法分配律计算二次根式的乘法可得.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{2}$+2=3$\sqrt{2}$+2;
(2)原式=$\sqrt{36}$-2$\sqrt{25}$=6-10=-4;
(3)原式=7-2$\sqrt{7}$+$\sqrt{7}$-2=5-$\sqrt{7}$;
(4)原式=20+25$\sqrt{6}$-4$\sqrt{10}$-10$\sqrt{15}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算,混合运算时注意运算顺序.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.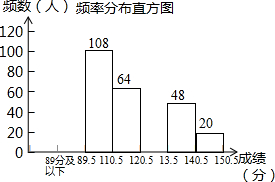 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
频率分布表
请你根据不完整的频率分布表,解答下列问题:
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:频率分布表
| 分组 | 频数 | 频率 |
| 89分及以下 | ||
| 89.5-110.5 | 108 | |
| 110.5-120.5 | 64 | 0.16 |
| 120.5-130.5 | 0.20 | |
| 130.5-140.5 | 48 | |
| 140.5-150.5 | 20 | 0.05 |
| 合计 | 400 | 1 |
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
 如图,当具备什么条件时,AB∥EF?请说明理由(写出一个即可)
如图,当具备什么条件时,AB∥EF?请说明理由(写出一个即可)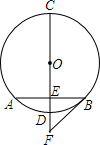 如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$.
如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$.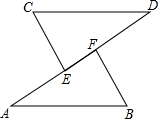 如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.
如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.