题目内容
7. 如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15cm,AB=9cm.求:
如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15cm,AB=9cm.求:(1)FC的长,
(2)EF的长.
分析 (1)由折叠性质可得AF=AD,由勾股定理可求出BF的值,再由FC=BC-BF求解即可;
(2)由题意得EF=DE,设DE的长为x,则EC的长为(9-x)cm,在Rt△EFC中,由勾股定理即可求得EF的值.
解答 解:(1)由题意得:AF=AD=15,
在Rt△ABF中,
∵AB=9,
∴$BF=\sqrt{A{F^2}-A{B^2}}=12$(cm)
∴FC=BC-BF=15-12=3(cm);
(2)由题意得:EF=DE,
设DE的长为x,则EC的长为(9-x)cm,
在Rt△EFC中,由勾股定理可得:(9-x)2+32=x2,
解得x=5,
即EF=5(cm).
点评 本题主要考查了折叠问题,解题的关键是熟记折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
12.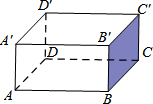 如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )
如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )
 如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )
如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )| A. | $\sqrt{53}$cm | B. | $\sqrt{45}$cm | C. | $\sqrt{41}$cm | D. | 7cm |
17.菱形ABCD的周长是20,对角线AC=8,则菱形ABCD的面积是( )
| A. | 12 | B. | 24 | C. | 40 | D. | 48 |
 在如图所示的平面直角坐标系中表示下面各点:
在如图所示的平面直角坐标系中表示下面各点: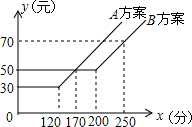 某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题:
某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题: