题目内容
16.一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,搅匀之后,每次摸出一只小球不放回.在连续2次摸出的都是黑球的情况下,第3次摸出黑球的概率是$\frac{3}{8}$.分析 让剩余黑球的个数除以剩余球的总数即为所求的概率.
解答 解:袋中有2个红球,3个白球和5个黑球,共10球,
则每次摸出一只小球不放回,在连续2次摸出的都是黑球的情况下,第3次摸出黑球的概率是:$\frac{5-2}{10-2}$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 本题考查了随机事件概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
6.在下列运算中,正确的是( )
| A. | (x4)2=x6 | B. | x3•x2=x6 | C. | x2+x2=2x4 | D. | x6÷x2=x4 |
11.冰柜里有四种饮料:2瓶可乐、3瓶咖啡、4瓶桔子水、6瓶汽水,其中可乐和咖啡是含有咖啡因的饮料,那么从冰柜里随机取一瓶饮料,该饮料含有咖啡因的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
 如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15cm,AB=9cm.求:
如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15cm,AB=9cm.求:
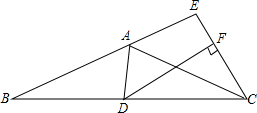 如图,等腰△ABC中,AB=AC,∠BAD=60°,将射线CA绕点C顺时针旋转交BA的延长线于点E,且∠ACE=$\frac{1}{2}$∠DAC,过点D作DF⊥CE于点F交AC于点G,若AB=5,AD=2,则AE=3.
如图,等腰△ABC中,AB=AC,∠BAD=60°,将射线CA绕点C顺时针旋转交BA的延长线于点E,且∠ACE=$\frac{1}{2}$∠DAC,过点D作DF⊥CE于点F交AC于点G,若AB=5,AD=2,则AE=3.