题目内容
11.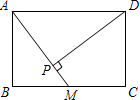 如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,则点D到AM的距离DP的长为$\frac{24}{5}$.
如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,则点D到AM的距离DP的长为$\frac{24}{5}$.
分析 根据矩形的性质可证明△ABM∽△DPA,再由相似三角形的性质可求得DP的长.
解答 解:∵四边形ABCD为矩形,
∴∠BAD=∠B=90°,
∴∠DAP+∠BAM=∠BAM+∠AMB,
∴∠DAP=∠AMB,
又PD⊥AM
∴∠B=∠APD,
∴△ABM∽△DPA,
∴$\frac{AB}{PD}$=$\frac{AM}{AD}$,
∵AD=BC,M为BC中点,
∴AD=6,BM=3,
在Rt△ABM中,由勾股定理可得AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴$\frac{4}{PD}$=$\frac{5}{6}$
∴PD=$\frac{24}{5}$,
故答案为:$\frac{24}{5}$.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形的对应边的比相等是解题的关键.

练习册系列答案
相关题目
3. 如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
 如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )| A. | 400cm2 | B. | 500cm2 | C. | 600cm2 | D. | 300cm2 |
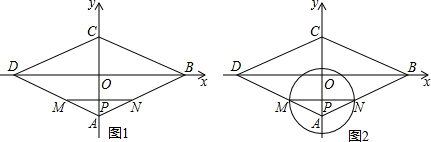
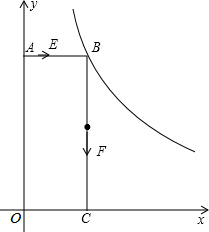 如图,已知:矩形AOCB的顶点B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且AB=3,BC=8.
如图,已知:矩形AOCB的顶点B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且AB=3,BC=8.