Question

6．如图，在平行四边形ABCD中，AE、BF、CF、DE分别为∠DAB、∠ABC、∠BCD、∠CDA的平分线．
（1）试猜想EF与AB的位置关系，并证明你的结论．
（2）试判断EF与AB、AD之间的数量关系．

Answer 1

分析 （1）延长DE交AB于G，延长BF交CD于H，由DE是∠CDA的平分线，BF是∠ABC的平分线，得到∠ABF=$\frac{1}{2}∠$ABC，∠CDG=$\frac{1}{2}∠$ADC，根据四边形ABCD 是平行四边形，得到∠ADC=∠ABC，推出DG∥BH，根据已知条件得到AE⊥DG，得到E是DG的中点，同理F是BH的中点，即可得到结论；
（2）根据EF∥BG，BF∥EG，得到四边形BFEG是平行四边形，根据平行四边形的性质得到EF=BG，根据等腰三角形的性质得到AD=AG，即可得到结论．

解答 解：（1）EF∥AB，
理由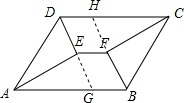：延长DE交AB于G，延长BF交CD于H，
∵DE是∠CDA的平分线，BF是∠ABC的平分线，
∴∠ABF=$\frac{1}{2}∠$ABC，∠CDG=$\frac{1}{2}∠$ADC，
∵四边形ABCD 是平行四边形，
∴∠ADC=∠ABC，
∴∠ABF=∠CDE，
∵AB∥CD，
∴∠CDE=∠AGD，
∴∠AGD=∠ABH，
∴DG∥BH，
∵AE、DE分别为∠DAB、∠CDA的平分线，∠CDA+∠DAB=180°，
∴AE⊥DG，
∴E是DG的中点，
同理F是BH的中点，
∴EF∥AB；

（2）EF=AB-AD，
理由：∵EF∥BG，BF∥EG，
∴四边形BFEG是平行四边形，
∴EF=BG，
∵∠CDE=∠ADE=∠AGE，
∴AD=AG，
∴BG=AB-AD，
∴EF=AB-AD．

点评 本题考查了平行四边形的判定和性质，角平分线的定义，等腰三角形的判定和性质，正确的作出辅助线构造平行四边形是解题的关键．