题目内容
16．解关于x的不等式．（1）$\frac{3x+5}{2x-1}$＞0
（2）|2x-3|≥5．
分析 （1）利用分子分母同号把原不等式转化为得$\left\{\begin{array}{l}{3x+5＞0}\\{2x-1＞0}\end{array}\right.$或$\left\{\begin{array}{l}{3x+5＜0}\\{2x-1＜0}\end{array}\right.$，然后分别解两个不等式组即可；
（2）根据绝对值的意义把原不等式转化为2x-3≥5或2x-3≤-5，然后分别解两个不等式即可．
解答 解：（1）根据题意得$\left\{\begin{array}{l}{3x+5＞0}\\{2x-1＞0}\end{array}\right.$或$\left\{\begin{array}{l}{3x+5＜0}\\{2x-1＜0}\end{array}\right.$，
所以x＞$\frac{1}{2}$或x＜-$\frac{5}{3}$；
（2）根据题意得2x-3≥5或2x-3≤-5，
所以x≥4或x≤-1．
点评 本题考查了解一元一次不等式：根据不等式的性质解一元一次不等式基本操作方法与解一元一次方程基本相同，都有如下步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
7．
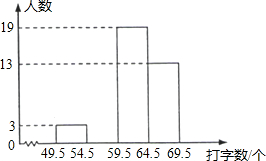初三（1）班共有40名同学，在一次30秒打字速度测试中他们的成绩统计如表：
（1）将这些数据按组距5（个字）分组，绘制成如图的频数分布直方图（不完整），请将表中空缺的数据填写完整，并补全频数分布直方图；
（2）若将频数分布直方图转化为扇形统计图，则打字数在54.5-59.5这一段所在扇形的圆心角的度数是多少？
初三（1）班共有40名同学，在一次30秒打字速度测试中他们的成绩统计如表：| 打字数/个 | 50 | 51 | 59 | 62 | 64 | 66 | 69 |
| 人数 | 1 | 2 | 8 | 11 | 5 |
（2）若将频数分布直方图转化为扇形统计图，则打字数在54.5-59.5这一段所在扇形的圆心角的度数是多少？
如图，已知△ABC，求作BC边上的高．（尺规作图，保留痕迹）
如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$（x＞0）的图象交于点P（n，2），与x轴交于点A，与y轴交于点C，PB⊥x轴于点B，且AC=BC，S△PBC=4．
如图，若点A的坐标为$（1，\sqrt{3}）$，则sin∠1=$\frac{{\sqrt{3}}}{2}$．
如图，在正方形ABCD中，AB=2，CA=CE，则△ACE的面积是2$\sqrt{2}$．
如图，在平行四边形ABCD中，AE、BF、CF、DE分别为∠DAB、∠ABC、∠BCD、∠CDA的平分线．