题目内容
18.已知x>0,y>0,且x-5$\sqrt{xy}$-6y=0,求$\frac{x-2\sqrt{xy}+y}{x+\sqrt{xy}-2y}$的值.分析 x-5$\sqrt{xy}$-6y=0即($\sqrt{x}-6\sqrt{y}$)($\sqrt{x}$+$\sqrt{y}$)=0,据此即可得到x=36y,然后代入所求的代数式即可求解.
解答 解:x-5$\sqrt{xy}$-6y=0即($\sqrt{x}-6\sqrt{y}$)($\sqrt{x}$+$\sqrt{y}$)=0,
∵x>0,y>0,
∴$\sqrt{x}-6\sqrt{y}$=0,
则x=36y,
则原式=$\frac{36y-12y+y}{36y+6y-2y}$=$\frac{25y}{40y}$=$\frac{5}{8}$.
点评 本题考查了二次根式的化简求值,正确把已知的式子进行变形,求得x=36y是解决本题的关键.

练习册系列答案
相关题目
8.下列几项调查中,适合使用普查的是( )
| A. | 调查我区奶制品中蛋白质含量是否达到国家标准 | |
| B. | 调查我区6月1日这天嘉陵江水中氨氮含量是否超标 | |
| C. | 调查我校初三某班全体学生的视力状况 | |
| D. | 调查我区市民对消防安全知识的知晓情况 |
10.在同一平面直角坐标系中,直线y=x与双曲线y=-$\frac{1}{x}$的交点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 不能确定 |
8.我国南海海域面积为3800000km2,用科学记数法表示正确的是( )
| A. | 3.8×105km2 | B. | 3.8×106km2 | C. | 3.8×107km2 | D. | 3.8×108km2 |
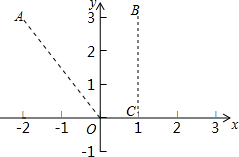 对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.
对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.