题目内容
10.在同一平面直角坐标系中,直线y=x与双曲线y=-$\frac{1}{x}$的交点个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 不能确定 |
分析 联立两函数解析式,可得该方程组无解,可判断没有交点.
解答 解:联立直线和双曲线的解析式可得$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{x}}\end{array}\right.$,
消去y整理可得x2+1=0,该方程无解.
故直线y=x与双曲线y=-$\frac{1}{x}$的交点个数为0.
故选A.
点评 本题主要考查函数图象的交点问题,掌握求函数图象交点的方法是解题的关键,即联立两函数解析式求其方程组的解.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
15.-4的相反数是( )
| A. | -4 | B. | 4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
20.计算:(-2)0=( )
| A. | -2 | B. | 2 | C. | 1 | D. | 0 |
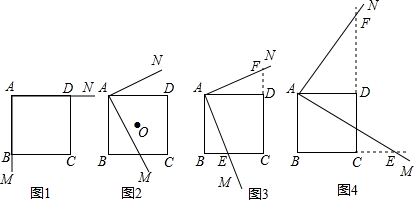
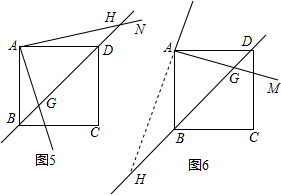
 如图,两个正方形边长分别是10厘米和6厘米,求阴影部分的面积.
如图,两个正方形边长分别是10厘米和6厘米,求阴影部分的面积.