题目内容
16.若关于x的方程(k-3)x2-$\sqrt{1+2k}$x+1=0有实数根,求k的取值范围.分析 要分类讨论:若k-3=0,而-$\sqrt{1+2k}$≠0,原方程变为一元一次方程,有解;当k-3≠0,原方程变为一元二次方程,如果△≥0,即△=1+2k-4(k-3)≥0,且1+2k≥0方程有实数根,得到-$\frac{1}{2}$≤k≤$\frac{13}{2}$,且k≠3,最后综合得到k的取值范围.
解答 解:当k-3≠0,即k≠3时,方程是一元二次方程,
由关于x的方程(k-3)x2-$\sqrt{1+2k}$x+1=0有实数根,得
△=(-$\sqrt{1+2k}$)2-4(k-3)=-2k+13≥0,且1+2k≥0,
解得-$\frac{1}{2}$≤k≤$\frac{13}{2}$;
当k-3=0,即k=3时,方程是一元一次方程,方程有实数根,
综上所述:当-$\frac{1}{2}$≤k≤$\frac{13}{2}$,关于x的方程(k-3)x2-$\sqrt{1+2k}$x+1=0有实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元一次方程和一元二次方程的定义,二次根式的定义以及分类讨论思想的运用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5.数学翻译 牛顿是举世闻名的伟大数学家、物理学家,他创立了微积分(另一个创立者是莱布尼茨)、经典力学,在代数学、光学、天文学等方面也作出了重要贡献,牛顿用数学的语言、方法描述和研究自然规律,他呕心沥血,写成的光辉著作《自然哲学的数学原理》,照亮了人类科学文明的大道,牛顿在他的《普遍的算术》一书中写道:“要解答一个含有数量间的抽象关系的问题,只要把题目由日常的语言译成代数的语言就行了.”下表是由牛顿给出的1个例子改写、简化而成的,请将表的空白补上(不必化简).
根据上表中的(3)可解得x=400.
| 日常语言 | 代数语言 |
| 一个商人有一笔钱 | x |
| 第一年他花去了100镑 | x-100 |
| 补进去余额的$\frac{1}{3}$ | (x-100)+$\frac{1}{3}$(x-100) |
| 第二年他又花去了100镑 | (1)(x-100)+$\frac{1}{3}$(x-100)-100 |
| 又补进去余额的$\frac{1}{3}$ | (2)(x-100)+$\frac{1}{3}$(x-100)-100+$\frac{1}{3}$[(x-100)+$\frac{1}{3}$(x-100)-100] |
| 结果他的钱数正好是原来的钱数 | (3)(x-100)+$\frac{1}{3}$(x-100)-100+$\frac{1}{3}$[(x-100)+$\frac{1}{3}$(x-100)-100]=x |
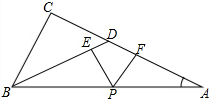 已知,如图,在△ABC中,∠C=90°,点D、P分别在边AC、AB上,且BD=AD,PE⊥BD,PF⊥AD,垂足分别为点E、F.
已知,如图,在△ABC中,∠C=90°,点D、P分别在边AC、AB上,且BD=AD,PE⊥BD,PF⊥AD,垂足分别为点E、F.