题目内容
9.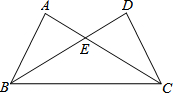 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°,求∠EBC的度数.
分析 (1)根据AAS即可推出△ABE和△DCE全等;
(2)根据三角形全等得出EB=EC,推出∠EBC=∠ECB,根据三角形的外角性质得出∠AEB=2∠EBC,代入求出即可.
解答 (1)证明:在△ABE和△DCE中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠AEB=∠DEC}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△DCE(AAS);
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
点评 本题考查了三角形外角性质和全等三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.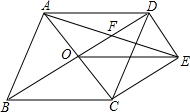 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | $2\sqrt{2}$ |
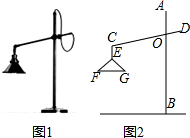 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.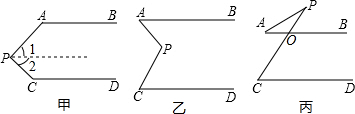 阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.
阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.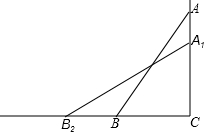 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?