题目内容
19.已知实数a满足|a-1|+$\sqrt{a-2}$=a,求a的值.分析 根据二次根式有意义的条件可得a-2≥0,解不等式可得a的取值范围,进而可得a-1>0,根据绝对值的性质可得a-1+$\sqrt{a-2}$=a,整理可得$\sqrt{a-2}$=1,进而可得a的值.
解答 解:根据二次根式有意义的条件可得a-2≥0,
解得:a≥2,
|a-1|+$\sqrt{a-2}$=a,
a-1+$\sqrt{a-2}$=a,
$\sqrt{a-2}$=1,
a=3.
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
相关题目
9.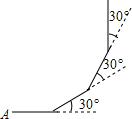 如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
 如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
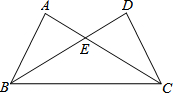 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.