题目内容
13. 如图,在△ABC中,∠ACB=90°,AB=5,tanA=$\frac{1}{2}$,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E;
如图,在△ABC中,∠ACB=90°,AB=5,tanA=$\frac{1}{2}$,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E;(1)求△ABC的面积;
(2)求sin∠CBE的值.
分析 (1)根据∠A的正切用BC表示出AC,再利用勾股定理列方程求出BC,再求出AC,然后根据直角三角形的面积公式列式计算即可得解;
(2)设CE=x,表示出AE,再根据翻折变换的性质可得BE=AE,然后列方程求出x,再利用锐角的正弦等于对边比斜边列式计算即可得解.
解答 解:(1)∵∠ACB=90°,tanA=$\frac{1}{2}$,
∴$\frac{BC}{AC}$=$\frac{1}{2}$,
∴AC=2BC,
在Rt△ABC中,BC2+AC2=AB2,
即BC2+4BC2=25,
解得BC=$\sqrt{5}$,
所以,AC=2$\sqrt{5}$,
△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×$\sqrt{5}$×2$\sqrt{5}$=5;
(2)设CE=x,则AE=AC-CE=2$\sqrt{5}$-x,
∵△ABC沿直线l翻折点A与点B重合,
∴BE=AE=2$\sqrt{5}$-x,
在Rt△BCE中,BC2+CE2=BE2,
即$\sqrt{5}$2+x2=(2$\sqrt{5}$-x)2,
解得x=$\frac{3\sqrt{5}}{4}$,
所以,CE=$\frac{3\sqrt{5}}{4}$,
BE=2$\sqrt{5}$-x=2$\sqrt{5}$-$\frac{3\sqrt{5}}{4}$=$\frac{5\sqrt{5}}{4}$,
所以,sin∠CBE=$\frac{CE}{BE}$=$\frac{\frac{3\sqrt{5}}{4}}{\frac{5\sqrt{5}}{4}}$=$\frac{3}{5}$.
点评 本题考查了翻折变换的性质,锐角三角函数的定义,此类题目,利用勾股定理列出方程求出相关的线段的长度是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | x2+y2+2x+2y | B. | x2+y2+2xy-2 | C. | x2-y2+4x+4y | D. | x2-y2+4y-4 |
| 种子粒数 | 100 | 400 | 800 | 1000 | 2000 | 5000 |
| 发芽种子粒数 | 85 | 298 | 652 | 793 | 1604 | 4005 |
| 发芽种子频率 | 0.850 | 0.745 | 0.815 | 0.793 | 0.802 | 0.801 |
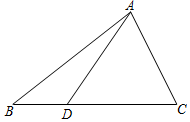 如图,已知点D是△ABC的边BC上一点,且BD=$\frac{1}{2}$CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,已知点D是△ABC的边BC上一点,且BD=$\frac{1}{2}$CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$. 如图,抛物线y=$\frac{1}{3}$x2+bx-1与x轴分别相交于点A、B,与y轴相交于点C,且OA=OC.
如图,抛物线y=$\frac{1}{3}$x2+bx-1与x轴分别相交于点A、B,与y轴相交于点C,且OA=OC.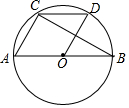 如图,AB为⊙O的直径,菱形AODC的顶点A,C,D在⊙O上,连接BC,则∠ABC的度数为30°.
如图,AB为⊙O的直径,菱形AODC的顶点A,C,D在⊙O上,连接BC,则∠ABC的度数为30°.