题目内容
9.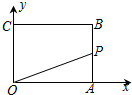 如图,已知矩形OABC,A(6,0),C(0,4),动点P从点A出发,沿A-B-C的路线以每秒2个单位长度的速度运动,设线段OP在运动过程中扫过矩形的面积为S,则下列能大致反映面积S与运动时间t(秒)之间关系的图象是( )
如图,已知矩形OABC,A(6,0),C(0,4),动点P从点A出发,沿A-B-C的路线以每秒2个单位长度的速度运动,设线段OP在运动过程中扫过矩形的面积为S,则下列能大致反映面积S与运动时间t(秒)之间关系的图象是( )| A. |  | B. | 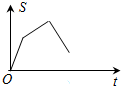 | C. | 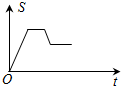 | D. |  |
分析 根据题意可以求出各段的函数解析式,从而可以得到相应的函数图象,从而可以解答本题.
解答 解:当0≤t≤2时,
S=$\frac{OA•AP}{2}=\frac{6×2t}{2}=6t$,
当2<t≤5时,
S=6×4-$\frac{(6+4-2t)×4}{2}$=4t+4,
由上可得,能大致反映面积S与运动时间t(秒)之间关系的图象是D中的函数图象,
故选D.
点评 本题考查动点问题的函数图象,解答本题的关键是明确题意,求出各段的函数解析式,利用数形结合的思想解答.

练习册系列答案
相关题目
17.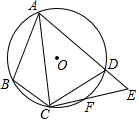 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )
 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
1.已知m2-4m=7,则代数式2m2-8m-13的值为( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
18.下列计算正确的是( )
| A. | 3$\sqrt{2}$+4$\sqrt{3}$=7$\sqrt{5}$ | B. | 5$\sqrt{2}$-3$\sqrt{2}$=2$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | D. | 6$\sqrt{5}$÷2$\sqrt{5}$=3$\sqrt{5}$ |
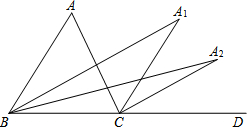 如图,∠ACD是△ABC的外角,第1次操作:∠ABC的平分线与∠ACD的平分线交于点A1;第2次操作:∠A1BC的平分线与∠A1CD的平分线交于点A2,…第n次操作:∠An-1BC的平分线与∠An-1CD的平分线交于点An,则∠A2与∠A之间的数量关系是∠A2=$\frac{1}{4}$∠A;若∠A=64°,∠An≤4°,则n的取值范围是n≥4.
如图,∠ACD是△ABC的外角,第1次操作:∠ABC的平分线与∠ACD的平分线交于点A1;第2次操作:∠A1BC的平分线与∠A1CD的平分线交于点A2,…第n次操作:∠An-1BC的平分线与∠An-1CD的平分线交于点An,则∠A2与∠A之间的数量关系是∠A2=$\frac{1}{4}$∠A;若∠A=64°,∠An≤4°,则n的取值范围是n≥4.
 如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是5$\sqrt{2}$.
如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是5$\sqrt{2}$.