题目内容
10.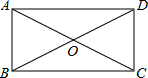 如图,矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若AB=1,则BC=$\sqrt{3}$.
如图,矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若AB=1,则BC=$\sqrt{3}$.
分析 由矩形的性质得出OA=OB,再由已知条件得出△AOB是等边三角形,得出OA=AB=1,AC=2,由勾股定理求出BC即可.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=1,
∴AC=2OA=2,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
2.在三边分别为下列长度的三角形中,不是直角三角形的是( )
| A. | 9,12,15 | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 2,3,$\sqrt{5}$ | D. | 4,7,5 |
 如图是某几何体的三视图,其中主视图是等边三角形,则该几何体的体积是4$\sqrt{3}$.
如图是某几何体的三视图,其中主视图是等边三角形,则该几何体的体积是4$\sqrt{3}$. 尺规作图:已知:∠1,利用尺规作∠AOB,使∠AOB=2∠1.(要求:保留作图痕迹,不写作法)
尺规作图:已知:∠1,利用尺规作∠AOB,使∠AOB=2∠1.(要求:保留作图痕迹,不写作法)