Question

16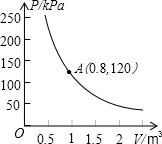．某气球内充满了一定质量的气体，当温度不变时，气球内的气压p（kpa）是气体体积v（m³）的反比例函数，其图象如图所示．
（1）写出这一函数的表达式．
（2）当气球体积为1.5m³时，气压是多少？
（3）当气球内的气压大于144kpa时，气球会爆炸，为了安全起见，气球的体积应不小于多少？

Answer 1

分析 （1）设函数解析式为P=$\frac{k}{v}$，把点（0.8，120）的坐标代入函数解析式求出k值，即可求出函数关系式；
（2）把V=1.5代入求得的函数关系式即可求出P值；
（3）依题意P≤144，即$\frac{96}{v}$≤144，解不等式即可．

解答 解：（1）设P与V的函数关系式为P=$\frac{k}{v}$，
则 $\frac{k}{0.8}$=120，
解得k=96，
∴函数关系式为P=$\frac{96}{V}$；

（2）当气球内气体的体积是1.5m³时，
P=$\frac{96}{1.5}$=64，
∴气球内气体的气压是64kPa．

（3）当P＞144KPa时，气球将爆炸，
∴P≤144，即$\frac{96}{v}$≤144，
解得V≥$\frac{2}{3}$（m³）．
故为了安全起见，气体的体积应不小于$\frac{2}{3}$（m³）．

点评 本题考查了反比例函数的实际应用，关键是建立函数关系式，并会运用函数关系式解答题目的问题．