题目内容
10.如图,在正五边形ABCDE中,AB=2.(1)如图1,将五边形ABCDE沿AD折叠,点E落在点E′处,连接BD
①填空:点E′与BD的位置关系是点E′在直线BD上;
②求BE′的长;
(2)如图2,点F在AB边上,且AF<$\frac{1}{2}$AB,沿DF折叠五边形ABCDE,点A,E的对应点分别为A′,E′,试猜想∠A′FB与∠E′DC有怎样的数量关系,并证明你的结论;
(3)如图3,分别连接AD,BD,点P在线段AD上运动(点P不与淀粉A,D重合),点Q在线段DB的延长线上运动,且AP=BQ,连接PQ交AB于点N,过点P作PM⊥AB于点M,在点P,Q运动的过程中,判断并证明线段MN的长是否发生变化.
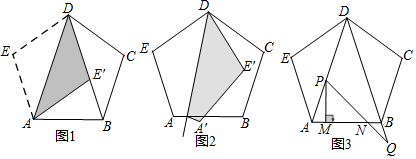
分析 (1)①利用正五边形的性质得出△DEA≌△DCB即可求出∠EDA=∠CDB=36°,进而即可得出结论;
②利用等腰三角形的性质得出AB=AE'=2,再判断出△ABE'∽△DBA,得出比例式求解即可得出结论;
(2)利用三角形的内角和和等腰三角形的性质即可求出∠CDE'=180°-2x=∠BFA',即可得出结论;
(3)先判断出△PMA≌△QHB得出MH=2,再判断出△PMN≌△NQH即可得出结论.
解答 解:(1)①点E′在直线BD上;理由如下:∵ABCDE是正五边形,
∴∠EDC=108°=∠DCB 且DC=CB,
∴∠CDB=36°,
在△DEA和△DCB中,$\left\{\begin{array}{l}{DE=DC}&{\;}\\{∠DEA=∠DCB}&{\;}\\{EA=CB}&{\;}\end{array}\right.$,
∴△DEA≌△DCB(SAS),
∴∠EDA=∠CDB=36°,
∴∠ADB=36°,
∴∠ADB=∠ADE'=36°,
∴B,D,E'共线,
即点E′在直线BD上;
故答案为:点E′在直线BD上;
②∵AD=BD,∠ADB=36°,
∴∠DAB=72°,
∵AE'=DE'.
∵AB=AE'=2,
∴DE'=2,
∴∠DAE=∠ADE',
∴∠BAE'=∠ADB,
∵∠ABD=∠ABE',
∴△ABE'∽△DBA,∴$\frac{AB}{DB}=\frac{BE′}{AB}$,
∴$\frac{2}{2+BE′}$=$\frac{BE′}{2}$,
∴BE'=$\sqrt{5}$-1;
(2)∵四边形内角和为360°,
设∠EDF=x,
∴∠AFD=144°-x=∠DFA',
∴∠DFB=36°+x,
∴∠A'FB=108°-2x,
且∠CDE'=108°-2x,
∴∠CDE'=∠BFA'
(3)如图3,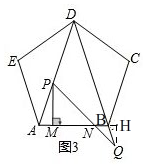 过点Q作QH⊥AB,
过点Q作QH⊥AB,
∵∠BAD=72°=∠DBA,
∴∠DAB=∠QBH且AP=BQ,∠AMP=∠BHQ
在△PMA和△QHB中,$\left\{\begin{array}{l}{∠PMA=∠QHB}&{\;}\\{∠PAM=∠QBH}&{\;}\\{AP=BQ}&{\;}\end{array}\right.$,
∴△PMA≌△QHB(AAS),
∴AM=BH,PM=QH,
∴MH=MB+BH=AM+MB=AB=2,
在△PMN和△NQH中,$\left\{\begin{array}{l}{∠PNM=∠QNH}&{\;}\\{∠PMN=∠QHN}&{\;}\\{PM=QH}&{\;}\end{array}\right.$,
∴△PMN≌△NQH(AAS),
∴MN=NH=1.
点评 此题是综合题目,考查了正五边形的性质,全等三角形的判定和性质,相似三角形的判定和性质,等腰三角形的判定和性质,解(1)的关键是得出∠ADB=∠ADE'=36°和△ABE'∽△DBA,解(2)的关键是∠DFB=36°+x,解(3)的关键是得出MH=AB=2,是一道中等难度的中考常考题.

 阅读快车系列答案
阅读快车系列答案| A. | 平均数 | B. | 方差 | C. | 中位数 | D. | 众数 |
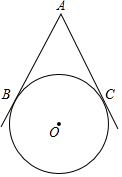 如图,AB、AC是◎o的两条切线,切点为B、C且∠BAC=50°,D是圆上一动点(不与B、C重合),则∠BDC的度数为( )
如图,AB、AC是◎o的两条切线,切点为B、C且∠BAC=50°,D是圆上一动点(不与B、C重合),则∠BDC的度数为( )| A. | 130° | B. | 65° | C. | 50°或130° | D. | 65°或115° |

 如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.
如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm. 如图,O为数轴原点,点A、B分别表示-2、2,以AB为底边向数轴上方作等腰三角形△ABC,连接OC,以O为圆心,OC长为半径画圆弧交数轴正半轴于点D,若AC=3,则点D表示的实数为$\sqrt{5}$.
如图,O为数轴原点,点A、B分别表示-2、2,以AB为底边向数轴上方作等腰三角形△ABC,连接OC,以O为圆心,OC长为半径画圆弧交数轴正半轴于点D,若AC=3,则点D表示的实数为$\sqrt{5}$.