题目内容
2．
如图，在直角三角尺ABC中，∠C=90°，把直角三角尺ABC放置在圆上，AB经过圆心O，AC与⊙O相交于D，E两点，点C，D，E的刻度分别是0cm，2cm，5cm，BC与⊙O相切于F点，那么⊙O的半径是3.5cm．
分析 如图连接OF，作OM⊥DE于M．，由∠C=∠CFO=∠CMO=90°，推出四边形CFOM是矩形，推出OF=CM，求出CM即可解决问题．
解答 解：如图连接OF，作OM⊥DE于M．
∵∠C=∠CFO=∠CMO=90°，
∴四边形CFOM是矩形，
∴OF=CM，
由题意可知CD=2，DE=3，∵OM⊥DE，
∴DM=ME=1.5，
∴OF=CM=CD+DM=3.5，
故答案为3.5
点评 本题考查切线的性质、垂径定理、矩形的判定和性质等知识，解题的关键是重合添加常用辅助线，灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
相关题目
17．
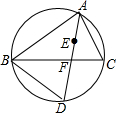如图，点E是△ABC的内心，AE的延长线与BC相交于点F，与△ABC的外接圆相交于点D，连接BD，且AB=AD，则∠ABC的度数为（ ）
如图，点E是△ABC的内心，AE的延长线与BC相交于点F，与△ABC的外接圆相交于点D，连接BD，且AB=AD，则∠ABC的度数为（ ）| A． | $\frac{3}{2}$∠D-90° | B． | 90°-$\frac{1}{2}$∠D | C． | 180°-∠D | D． | 3∠D-180° |
如图，一次函数y=ax+b的图象与x轴交于点A，与反比例函数y=$\frac{k}{x}$（x＜0）的图象交于点B（-2，n），过点B作BC⊥x轴于点C，点P（-4-n，1）是该反比例函数图象上的一点，且∠PBC=∠ABC，分别求反比例函数和一次函数的解析式．