题目内容
1．
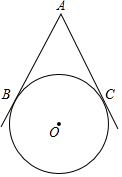如图，AB、AC是◎o的两条切线，切点为B、C且∠BAC=50°，D是圆上一动点（不与B、C重合），则∠BDC的度数为（ ）| A． | 130° | B． | 65° | C． | 50°或130° | D． | 65°或115° |
分析 如图连接OB、OC．首先求出∠BOC，再根据∠BD′C=$\frac{1}{2}$∠BOC，∠BDC+∠BD′C=180°，即可解决问题．
解答 解：如图连接OB、OC．
∵AB、AC是⊙O的切线，
∴OB⊥AB，OC⊥AC，
∴∠ABO=∠ACO=90°，
∵∠BAC=50°，
∴∠BOC=360°-90°-90°-50°=130°，
∴∠BD′C=$\frac{1}{2}$∠BOC=65°，
∴∠BCD=180°-65°=115°，
故选D．
点评 本题考查切线的性质、圆周角定理，圆内接四边形的性质等知识，解题的关键是学会添加常用辅助线，则有一题多解．
练习册系列答案
相关题目
16．考虑下面两种移动电话计费方式：
用函数方法解答何时两种计费方式费用相等．
| 方式一 | 方式二 | |
| 月租费/（元/月） | 30 | 0 |
| 本地通话费/（元/min） | 0.30 | 0.40 |
如图，一次函数y=ax+b的图象与x轴交于点A，与反比例函数y=$\frac{k}{x}$（x＜0）的图象交于点B（-2，n），过点B作BC⊥x轴于点C，点P（-4-n，1）是该反比例函数图象上的一点，且∠PBC=∠ABC，分别求反比例函数和一次函数的解析式．