题目内容
8.今年秋季,我县县城部分学校将准备搬迁新校舍,在迁入新校舍之前,某学校的同学们就该校学生如何到校问题进行了一次调查,并将调查结果制成了表格,条形图和扇形统计图,请你根据图表信息完成下列各题:(1)此次共调查了多少位学生?
(2)请将表格填充完整;
| 步行 | 骑自行车 | 坐公共汽车 | 其他 |
| 60 |
(4)如果该校共有1000名学生,请你计算该校步行和骑自行车的一共有多少人?
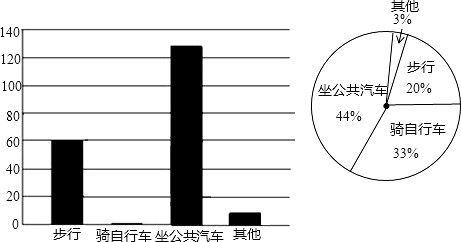
分析 (1)步行的有60人,所占百分比为20%,则可求出参与调查学生总数;
(2)求出骑自行车、坐公共汽车和其他的人数,补全表格即可;
(3)根据(2)的计算结果补全条形图;
(4)用1000乘以步行和骑自行车所占的百分比即可.
解答 解:(1)调查的学生人数为:60÷20%=300(人);
(2)300×33%=99(人),300×44%=132(人),300×3%=9(人),补充表格如下表:
| 步行 | 骑自行车 | 坐公共汽车 | 其他 |
| 60 | 99 | 132 | 9 |
 (4)1000×(20%+33%)=1000×55%=550(人),
(4)1000×(20%+33%)=1000×55%=550(人),∴该校骑自行车和步行的一共有550人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
18. 如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
 如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )| A. | 55° | B. | 65° | C. | 25° | D. | 35° |
19. 如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
 如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
16.某花卉基地种植了郁金香和玫瑰两种花卉共30亩,有关数据如表:
(1)设种植郁金香x亩,两种花卉总收益为y万元,求y关于x的函数关系式.(收益=销售额-成本)
(2)若计划投入的成本的总额不超过70万元,要使获得的收益最大,基地应种植郁金香和玫瑰个多少亩?
| 成本 (单位:万元/亩) | 销售额 (单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
(2)若计划投入的成本的总额不超过70万元,要使获得的收益最大,基地应种植郁金香和玫瑰个多少亩?
13.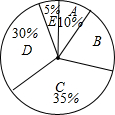 自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( )
自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( )
 自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( )
自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( ) | 组别 | 月用水量x(单位:吨) |
| A | 0≤x<3 |
| B | 3≤x<6 |
| C | 6≤x<9 |
| D | 9≤x<12 |
| E | x>12 |
| A. | 18户 | B. | 20户 | C. | 22户 | D. | 24户 |
20.某工厂共有60名员工,他们的月工资方差是s2,现在给每个员工的月工资增加300元,那么他们的新工资的方差( )
| A. | 变为s2+300 | B. | 不变 | C. | 变大了 | D. | 变小了 |
17.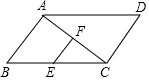 如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
 如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )| A. | 2.5 | B. | 5 | C. | 10 | D. | 15 |
18. 如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
 如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )| A. | 44° | B. | 46° | C. | 88° | D. | 54° |
 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(4,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-1,0)或(1,8).
如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(4,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-1,0)或(1,8).