题目内容
15.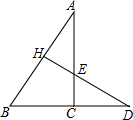 如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:
如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:(1)图中有几个直角三角形?
(2)∠AEH和∠B是什么关系?为什么?
(3)若∠B=70°,∠A和∠CED各是多少度?
分析 (1)根据直角三角形定义,从直角顶点考虑写出即可;
(2)根据同角的余角相等解答;
(3)根据直角三角形两锐角互余求出∠A,然后求出∠AEH,再根据对顶角相等求出∠CED.
解答 解:(1)∵DH⊥AB于H,
∴△AEH和△BDH是直角三角形,
∵AC⊥BD于C,
∴△ABC和△CDE是直角三角形,
所以,直角三角形有四个;
(2)∵DH⊥AB,AC⊥BD,
∴∠AEH+∠A=90°,∠B+∠A=90°,
∴∠AEH=∠B;
(3)∵AC⊥BD,
∴∠ACB=90°,
∴∠A=90°-∠B=90°-70°=20°,
由(2)可知,∠AEH=∠B=70°,
所以,∠CED=∠AEH=70°(对顶角相等).
点评 本题考查了直角三角形两锐角互余的性质,同角的余角相等的性质,以及直角三角形的定义,是基础题,熟记各性质并准确识图是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
20.某市为了加快城市建设力度.2014年市政府共投资2亿元人民币,预计到2016年底三年共累计投资9.5亿元人民币,若在这两年内每年投资的增长率都为x,可列方程( )
| A. | 2x2=9.5 | B. | 2+2(x+1)+2(x+1)2=9.5 | ||
| C. | 2(x+1)2=9.5 | D. | 2+(x+1)+(x+1)2=9 |
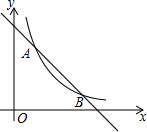 如图,一次函数y=kx+b(k、b为常数,且k≠0)的图象与反比例函数y=$\frac{3}{x}$的图象交于A(1,a),B(3,1)两点.
如图,一次函数y=kx+b(k、b为常数,且k≠0)的图象与反比例函数y=$\frac{3}{x}$的图象交于A(1,a),B(3,1)两点.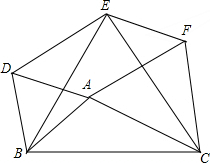 如图所示,以△ABC的三边AB、BC、CA在BC的同侧作等边△ABD、△BCE、△CAF
如图所示,以△ABC的三边AB、BC、CA在BC的同侧作等边△ABD、△BCE、△CAF 如图,AB、CD相交于点O,EO⊥DC,∠AOE的余角是∠AOD,∠COB的补角是∠AOC和∠BOD.
如图,AB、CD相交于点O,EO⊥DC,∠AOE的余角是∠AOD,∠COB的补角是∠AOC和∠BOD.